Batting Averages
In this topic, you will apply your knowledge of percentages and mean to baseball.
Example 1:
In 530 at bats, a baseball player has a batting average of 0.241. In the next game, he has 4 at bats. What is the most likely number of hits he will get?
Suppose he hits 3 of those swings. What is his new batting average to three places?
Part 1: Most likely number of hits
The baseball player has a batting average of 0.241 after 530 at bats. This means that he has a 24.1% chance of getting a hit whenever he swings at a ball.
1. The most likely number of hits is the number of hits × batting average.
So for the next 4 hits, the most likely number of hits is 4 × 0.241 = 0.964
2. We then round to the nearest whole number of hits.
0.964 hits rounds to 1 hit
Part 2: New batting average
Batting average =
We calculate the new batting average using the fact that after his 530 at bats, the baseball player made 3 more hits from 4 more swings.
New batting average =
=
Original number of hits = original batting average × original number of swings
= 0.241 × 530
= 127.73 which rounds to 128
New batting average =
=
= 0.245
Most likely number of hits: 1
New batting average: 0.245
Sample Problems For Batting Averages
________________________________________
Complexity=0
Answer the following questions about batting averages.
1. In 171 at bats, a baseball player has a batting average of 0.391. In the next game, he has 2 at bats. What is the most likely number of hits he will get?
Suppose he hits 1 of those swings. What is his new batting average to three places?
2. In 303 at bats, a baseball player has a batting average of 0.354. In the next game, he has 5 at bats. What is the most likely number of hits he will get?
Suppose he hits 0 of those swings. What is his new batting average to three places?
________________________________________
Complexity=1
Answer the following questions about batting averages.
1. In 126 at bats, a baseball player has a batting average of 0.301. In the next game, he has 2 at bats. What is the most likely number of hits he will get?
Suppose he hits 1 of those swings. What is his new batting average to three places?
2. In 272 at bats, a baseball player has a batting average of 0.363. In the next game, he has 3 at bats. What is the most likely number of hits he will get?
Suppose he hits 0 of those swings. What is his new batting average to three places?
________________________________________
Complexity=2
Answer the following questions about batting averages.
1. In 415 at bats, a baseball player has a batting average of 0.202. In the next game, he has 2 at bats. What is the most likely number of hits he will get?
Suppose he hits 2 of those swings. What is his new batting average to three places?
2. In 381 at bats, a baseball player has a batting average of 0.316. In the next game, he has 4 at bats. What is the most likely number of hits he will get?
Suppose he hits 4 of those swings. What is his new batting average to three places?
Answers
________________________________________
Complexity=0
Solution
The player's batting average is 0.391 and the number of swings is 2.
0.391 × 2 = 0.782 which rounds to 1.
Original total number of hits = batting average * total swings = 0.391 × 171 = 67.
New total number of hits = original number of hits + number of hits at next game = 67 + 1 = 68.
New total number of swings = original number of swings + number of swings at next game = 171 + 2 = 173.
New batting average = new total number of hits / new total number of swings = 68 / 173 = 0.393.
Solution
The player's batting average is 0.354 and the number of swings is 5.
0.354 × 5 = 1.77 which rounds to 2.
Original total number of hits = batting average * total swings = 0.354 × 303 = 107.
New total number of hits = original number of hits + number of hits at next game = 107 + 0 = 107.
New total number of swings = original number of swings + number of swings at next game = 303 + 5 = 308.
New batting average = new total number of hits / new total number of swings = 107 / 308 = 0.347.
________________________________________
Complexity=1
Solution
The player's batting average is 0.301 and the number of swings is 2.
0.301 × 2 = 0.602 which rounds to 1.
Original total number of hits = batting average * total swings = 0.301 × 126 = 38.
New total number of hits = original number of hits + number of hits at next game = 38 + 1 = 39.
New total number of swings = original number of swings + number of swings at next game = 126 + 2 = 128.
New batting average = new total number of hits / new total number of swings = 39 / 128 = 0.305.
Solution
The player's batting average is 0.363 and the number of swings is 3.
0.363 × 3 = 1.089 which rounds to 1.
Original total number of hits = batting average * total swings = 0.363 × 272 = 99.
New total number of hits = original number of hits + number of hits at next game = 99 + 0 = 99.
New total number of swings = original number of swings + number of swings at next game = 272 + 3 = 275.
New batting average = new total number of hits / new total number of swings = 99 / 275 = 0.360.
________________________________________
Complexity=2
Solution
The player's batting average is 0.202 and the number of swings is 2.
0.202 × 2 = 0.404 which rounds to 0.
Original total number of hits = batting average * total swings = 0.202 × 415 = 84.
New total number of hits = original number of hits + number of hits at next game = 84 + 2 = 86.
New total number of swings = original number of swings + number of swings at next game = 415 + 2 = 417.
New batting average = new total number of hits / new total number of swings = 86 / 417 = 0.206.
Solution
The player's batting average is 0.316 and the number of swings is 4.
0.316 × 4 = 1.264 which rounds to 1.
Original total number of hits = batting average * total swings = 0.316 × 381 = 120.
New total number of hits = original number of hits + number of hits at next game = 120 + 4 = 124.
New total number of swings = original number of swings + number of swings at next game = 381 + 4 = 385.
New batting average = new total number of hits / new total number of swings = 124 / 385 = 0.322.
Monday, November 10, 2008
Tuesday, November 4, 2008
Tally and Pictographs
To better understand the data you collect, you can use tally tables or pictographs to organize your data.
Example:
A class did a survey of the students' favorite drinks.
Here is the data they collected: The same data can be shown in a tally table OR a pictograph.


Tally Tables
For tally tables, each | represents one.
To count tallies faster, skip count by 5 for each .
Pictographs
Always remember to look at the Key so you know what each pictures means.
For example,



1.How many people voted for hip hop?
basket ball
baseball
soccer
2.How many total people voted for hip hop or classical?

1.Order the following (1, 2, or 3) from the most popular to the least popular.
2.If 17 students signed up for dodgeball, how would this be displayed on the graph?

1.Which type of movies is the most popular?
fantasy
comedy
drama
horror
foreign
romance
2.How many people voted for drama?

1.How many more students signed up for the most popular league than for the least popular league?
2.How many sign-ups were there in all?
Answers
1. How many people voted for hip hop?
2. How many total people voted for hip hop or classical?
Solution
hip hop + classical =
7 + 11 =
18
1.Order the following (1, 2, or 3) from the most popular to the least popular.
3 basketball
2 baseball
1 soccer
2. If 17 students signed up for dodgeball, how would this be displayed on the graph?

How many people voted for drama?
3 people
How many more students signed up for the most popular league than for the least popular league?
22 students
Solution
30 - 8 = 22
Soccer 22
Basketball 21
Baseball 8
How many sign-ups were there in all?
132sign-ups
Solution
22 + 8 + 22 + 29 + 21 + 30 = 132
Example:
A class did a survey of the students' favorite drinks.
Here is the data they collected: The same data can be shown in a tally table OR a pictograph.


Tally Tables
For tally tables, each | represents one.
To count tallies faster, skip count by 5 for each .
Pictographs
Always remember to look at the Key so you know what each pictures means.
For example,



1.How many people voted for hip hop?
basket ball
baseball
soccer
2.How many total people voted for hip hop or classical?

1.Order the following (1, 2, or 3) from the most popular to the least popular.
2.If 17 students signed up for dodgeball, how would this be displayed on the graph?

1.Which type of movies is the most popular?
fantasy
comedy
drama
horror
foreign
romance
2.How many people voted for drama?

1.How many more students signed up for the most popular league than for the least popular league?
2.How many sign-ups were there in all?
Answers
1. How many people voted for hip hop?
2. How many total people voted for hip hop or classical?
Solution
hip hop + classical =
7 + 11 =
18
1.Order the following (1, 2, or 3) from the most popular to the least popular.
3 basketball
2 baseball
1 soccer
2. If 17 students signed up for dodgeball, how would this be displayed on the graph?

How many people voted for drama?
3 people
How many more students signed up for the most popular league than for the least popular league?
22 students
Solution
30 - 8 = 22
Soccer 22
Basketball 21
Baseball 8
How many sign-ups were there in all?
132sign-ups
Solution
22 + 8 + 22 + 29 + 21 + 30 = 132
Bar grahp
Bar Graphs
A bar graph is one way to organize data.
The bars represent the data - the longer the bar, the larger the value of the data.

Pay attention to the scale of bar graphs.
The scale tells you the value of the length of the bars.
Example: Same graphs, different scales

This graph shows that
12 students like hip hop,
8 students like classical,
7 students like rock,
and 14 students like jazz.

This graph shows that
60 students like hip hop,
40 studnets like classical,
35 students like rock,
and 70 students like jazz.

1. Is this a vertical or horizontal bar graph?
vertical
horizontal
2. How many people voted for rock?

1. Which type of music is the least popular?
jazz
reggae
hip hop
Latin
R&B
2. Order the following (1, 2, or 3) from the most popular to the least popular.
Latin
hip hop
reggae

1. How many fewer pounds of apples were sold than grapes?
2. How many total pounds of fruit sold were lemons or cherries?

1. How many more people signed up for the most popular class than for the least popular class?
2. How many sign-ups were not for the astronomy class or the archery class?
Answers
1. Is this a vertical or horizontal bar graph?
horizontal
2. How many people voted for rock?
7 people
Which type of music is the least popular?
hip hop
Types of Music Number of Students
reggae 12
jazz 11
Latin 7
R&B 5
hip hop 4
Order the following (1, 2, or 3) from the most popular to the least popular.
2 Latin
3 hip hop
1 reggae
solution
reggae 12
jazz 11
Latin 7
R&B 5
hip hop 4
How many fewer pounds of apples were sold than grapes?
pounds of apples
Solution
grape - apple =11 - 6 = 5
How many total pounds of fruit sold were lemons or cherries?
pounds of fruit
Solution
lemon + cherry = 5 + 7 = 12
How many more people signed up for the most popular class than for the least popular class?
15 people
24 - 9 = 15
Classes Number of Sign-Ups
ballet 24
philosophy 23
watercolor 21
photography 15
archery 14
astronomy 9
How many sign-ups were not for the astronomy class or the archery class?
83 sign-ups
Solution
watercolor + philosophy + ballet + photography =
21 + 23 + 24 + 15 = 83
A bar graph is one way to organize data.
The bars represent the data - the longer the bar, the larger the value of the data.

Pay attention to the scale of bar graphs.
The scale tells you the value of the length of the bars.
Example: Same graphs, different scales

This graph shows that
12 students like hip hop,
8 students like classical,
7 students like rock,
and 14 students like jazz.

This graph shows that
60 students like hip hop,
40 studnets like classical,
35 students like rock,
and 70 students like jazz.

1. Is this a vertical or horizontal bar graph?
vertical
horizontal
2. How many people voted for rock?

1. Which type of music is the least popular?
jazz
reggae
hip hop
Latin
R&B
2. Order the following (1, 2, or 3) from the most popular to the least popular.
Latin
hip hop
reggae

1. How many fewer pounds of apples were sold than grapes?
2. How many total pounds of fruit sold were lemons or cherries?

1. How many more people signed up for the most popular class than for the least popular class?
2. How many sign-ups were not for the astronomy class or the archery class?
Answers
1. Is this a vertical or horizontal bar graph?
horizontal
2. How many people voted for rock?
7 people
Which type of music is the least popular?
hip hop
Types of Music Number of Students
reggae 12
jazz 11
Latin 7
R&B 5
hip hop 4
Order the following (1, 2, or 3) from the most popular to the least popular.
2 Latin
3 hip hop
1 reggae
solution
reggae 12
jazz 11
Latin 7
R&B 5
hip hop 4
How many fewer pounds of apples were sold than grapes?
pounds of apples
Solution
grape - apple =11 - 6 = 5
How many total pounds of fruit sold were lemons or cherries?
pounds of fruit
Solution
lemon + cherry = 5 + 7 = 12
How many more people signed up for the most popular class than for the least popular class?
15 people
24 - 9 = 15
Classes Number of Sign-Ups
ballet 24
philosophy 23
watercolor 21
photography 15
archery 14
astronomy 9
How many sign-ups were not for the astronomy class or the archery class?
83 sign-ups
Solution
watercolor + philosophy + ballet + photography =
21 + 23 + 24 + 15 = 83
Line Graphs

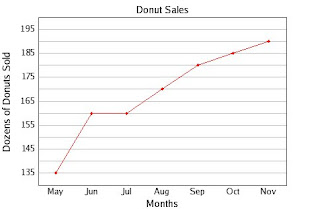
1.How many donuts were sold in July?
160 dozens
2.When were 185 dozen donuts sold? (check all that apply)
October
A line graph shows change over time.
The data is connected by lines, like dot-to-dot or connect-the-dots.
The x-axis (horizontal) usually has the time, increasing from left to right.
The y-axis (vertical) usually has the numbers that measure what is changing over time.
The bear population in the Emerald Forest increased over time.
Measurement - temp/mass/vol
Temperature Conversion - Celsius to Fahrenheit
The metric system uses the Celsius scale to measure temperature. However, temperatures are still measured on the Fahrenheit scale in the U.S.
Water freezes at 0o Celsius and boils at 100o Celsius which is a difference of 100o. Water freezes at 32o Fahrenheit and boils at 212o Fahrenheit which is a difference of 180o. Therefore each degree on the Celsius scale is equal to 180/100 or 9/5 degrees on the Fahrenheit scale.
* How to convert Celsius temperatures to Fahrenheit Multiply the Celsius temperature by 9/5.
* Add 32o to adjust for the offset in the Fahrenheit scale.
* Example: convert 37o C to Fahrenheit.
37 * 9/5 = 333/5 = 66.6
66.6 + 32 = 98.6o F
There is a mental math method to convert from Celsius to Fahrenheit. The ratio of 9/5 is equal to 1.8 and 1.8 is equivalent to 2 - 0.2
* How to convert Celsius temperatures to Fahrenheit with mental math. Double the Celsius temperature (multiply by 2).
* Take 1/10 of this number (2 * 1/10 = 0.2) and subtract it from the number above.
* Add 32o to adjust for the offset in the Fahrenheit scale.
*
* Example: convert 37o C to Fahrenheit.
37 * 2 = 74
74 * 1/10 = 7.4
74 - 7.4 = 66.6
66.6 + 32 = 98.6o F
Temperature Conversion - Celsius to Fahrenheit
The metric system uses the Celsius scale to measure temperature. However, temperatures are still measured on the Fahrenheit scale in the U.S.
Water freezes at 0o Celsius and boils at 100o Celsius which is a difference of 100o. Water freezes at 32o Fahrenheit and boils at 212o Fahrenheit which is a difference of 180o. Therefore each degree on the Celsius scale is equal to 180/100 or 9/5 degrees on the Fahrenheit scale.
* How to convert Celsius temperatures to Fahrenheit Multiply the Celsius temperature by 9/5.
* Add 32o to adjust for the offset in the Fahrenheit scale.
* Example: convert 37o C to Fahrenheit.
37 * 9/5 = 333/5 = 66.6
66.6 + 32 = 98.6o F
There is a mental math method to convert from Celsius to Fahrenheit. The ratio of 9/5 is equal to 1.8 and 1.8 is equivalent to 2 - 0.2
* How to convert Celsius temperatures to Fahrenheit with mental math. Double the Celsius temperature (multiply by 2).
* Take 1/10 of this number (2 * 1/10 = 0.2) and subtract it from the number above.
* Add 32o to adjust for the offset in the Fahrenheit scale.
*
* Example: convert 37o C to Fahrenheit.
37 * 2 = 74
74 * 1/10 = 7.4
74 - 7.4 = 66.6
66.6 + 32 = 98.6o F
Note: This lesson includes temperatures that use negative numbers. Negative numbers follow a pattern that is opposite of positive numbers. The number -20 is smaller than the number -10. Example of counting with negative and positive numbers: -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5.
* Example of converting negative Celsius temperatures to Fahrenheit Convert -15o C to Fahrenheit.
* -15 * 9/5 = -135/5 = -27
* -27 + 32 = 5o F
Temperature Conversion - Fahrenheit to Celsius
The metric system uses the Celsius scale to measure temperature. However, temperatures are still measured on the Fahrenheit scale in the U.S.
Water freezes at 0o Celsius and boils at 100o Celsius which is a difference of 100o. Water freezes at 32o Fahrenheit and boils at 212o Fahrenheit which is a difference of 180o. Therefore each degree on the Fahrenheit scale is equal to 100/180 or 5/9 degrees on the Celsius scale.
* How to convert Fahrenheit temperatures to Celsius Subtract 32o to adjust for the offset in the Fahrenheit scale.
* Multiply the result by 5/9.
* Example: convert 98.6o Fahrenheit to Celsius.
98.6 - 32 = 66.6
66.6 * 5/9 = 333/9 = 37o C.
There is a mental math method to approximate the Fahrenheit to Celsius conversion. The ratio of 5/9 is approximately equal to 0.55555....
* How to approximate the conversion of Fahrenheit temperatures to Celsius with mental math. Subtract 32o to adjust for the offset in the Fahrenheit scale.
* Divide the Celsius temperature by 2 (multiply by 0.5).
* Take 1/10 of this number (0.5 * 1/10 = 0.05) and add it from the number above.
* Example: convert 98.6o F to Celsius.
98.6 - 32 = 66.6
66.6 * 1/2 = 33.3
33.3 * 1/10 = 3.3
33.3 + 3.3 = 36.6 which is an approximation of the Celsius temperature
Temperature Conversion - Fahrenheit to Celsius
The metric system uses the Celsius scale to measure temperature. However, temperatures are still measured on the Fahrenheit scale in the U.S.
Water freezes at 0o Celsius and boils at 100o Celsius which is a difference of 100o. Water freezes at 32o Fahrenheit and boils at 212o Fahrenheit which is a difference of 180o. Therefore each degree on the Fahrenheit scale is equal to 100/180 or 5/9 degrees on the Celsius scale.
* How to convert Fahrenheit temperatures to Celsius Subtract 32o to adjust for the offset in the Fahrenheit scale.
* Multiply the result by 5/9.
* Example: convert 98.6o Fahrenheit to Celsius.
98.6 - 32 = 66.6
66.6 * 5/9 = 333/9 = 37o C.
There is a mental math method to approximate the Fahrenheit to Celsius conversion. The ratio of 5/9 is approximately equal to 0.55555....
* How to approximate the conversion of Fahrenheit temperatures to Celsius with mental math. Subtract 32o to adjust for the offset in the Fahrenheit scale.
* Divide the Celsius temperature by 2 (multiply by 0.5).
* Take 1/10 of this number (0.5 * 1/10 = 0.05) and add it from the number above.
* Example: convert 98.6o F to Celsius.
98.6 - 32 = 66.6
66.6 * 1/2 = 33.3
33.3 * 1/10 = 3.3
33.3 + 3.3 = 36.6 which is an approximation of the Celsius temperature
Note: This lesson includes temperatures that use negative numbers. Negative numbers follow a pattern that is opposite of positive numbers. The number -20 is smaller than the number -10. Example of counting with negative and positive numbers: -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5
* Example of converting negative Fahrenheit temperatures to Celsius Convert -4o F to Celsius.
* -4 - 32 = -36
* -36 * 5/9 = -180/9 = -20o C
Converting between Metric Units of Mass
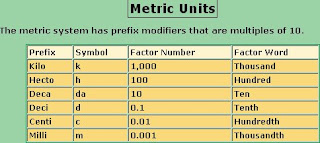
The metric system has prefix modifiers that are multiples of 10.
* A kilogram is 1000 grams
* A hectogram is 100 grams
* A decagram is 10 grams
* A gram is the stem unit of mass
* A decigram is 1/10 gram
* A centigram is 1/100 gram
* A milligram is 1/1000 gram
As we move down the units, the next unit is one tenth as heavy. As we move upward, each unit is 10 times as heavy. One hundred milligrams, which is 1/10 gram (100/1000=1/10) are heavier than one centigram (1/100th gram).
Comparing Mass in Grams
The metric system has prefix modifiers that are powers of 10.
* A kilogram is 1000 grams
* A hectogram is 100 grams
* A decagram is 10 grams
* A gram is the basic unit of mass
* A decigram is 1/10 gram
* A centigram is 1/100 gram
* A milligram is 1/1000 gram
Multiplying Pounds and Ounces
How to multiply pounds and ounces
* Convert pounds and ounces to ounces by multiplying pounds by 16 and adding the number of ounces
* Perform the required multiplication to determine the number of ounces.
* Convert the ounces to pounds and ounces by dividing by 16.
* The quotient is the number of pounds and the remainder is the number of ounces.
Example: Multiply 5 pounds 6 ounces times 4
* Convert 5 pounds to ounces by multiplying 16 by 5:
16 * 5 = 80 ounces
* Add the number of extra ounces:
80 + 6 = 86 ounces
* Perform the required multiplication:
86 * 4 = 344 ounces
* Convert to pounds and ounces by dividing by 16:
344 ÷ 16 = 21 R 8
* The quotient (21) is the number of pounds and the remainder (8) is the number of ounces.
* Answer: 21 pounds 8 ounces
Dividing Pounds and Ounces
How to divide pounds and ounces
* Convert pounds and ounces to ounces by multiplying pounds by 16 and adding the number of ounces
* Perform the required division to determine the number of ounces.
* Convert the ounces to pounds and ounces by dividing by 16.
* The quotient is the number of pounds and the remainder is the number of ounces.
Example: Divide 10 pounds 0 ounces by 4
* Convert 10 pounds to ounces by multiplying 10 by 16:
16 * 10 = 160 ounces
* Add the number of extra ounces:
160 + 0 = 160 ounces
* Perform the required division:
160 ÷ 4 = 40 ounces
* Convert to pounds and ounces by dividing by 16:
40 ÷ 16 = 2 R 8
* The quotient (2) is the number of pounds and the remainder (8) is the number of ounces.
* Answer: 2 pounds 8 ounces
Converting Metric Volume Units
The metric system has prefix modifiers that are multiples of 10.
* A kiloliter is 1000 liters
* A hectoliter is 100 liters
* A decaliter is 10 liters
* A liter is the basic unit of volume
* A deciliter is 1/10 liter
* A centiliter is 1/100 liter
* A milliliter is 1/1000 liter
As we move down the units, the next unit is one tenth as large. As we move upward, each unit is 10 times as large. One hundred milliliters, which is 1/10 liter (100/1000=1/10) are larger than one centiliter (1/100th liter).
Comparing Metric Liters
The metric system has prefix modifiers that are powers of 10.
* A kiloliter is 1000 liters
* A hectoliter is 100 liters
* A decaliter is 10 liters
* A liter is the basic unit of volume
* A deciliter is 1/10 liter
* A centiliter is 1/100 liter
* A milliliter is 1/1000 liter
Comparing Volume by Metric Prefixes
The metric system uses prefixes to indicate the size of the units of measurement. Each prefix varies from the next by a factor of ten. It is either ten times as large or one tenth the size.
The common prefixes with their values are:
* kilo = 1000
* hecto = 100
* deca = 10
* no prefix = 1
* deci = 1/10
* centi = 1/100
* milli = 1/1000
An example of comparing volume based on metric prefixes is: A deciliter is larger than a milliliter.
Multiplying Gallons, Quarts and Pints
How to multiply gallons, quarts and pints
* Convert gallons to pints by multiplying the number of gallons by 8.
* Convert quarts to pints by multiplying the number of quarts by 2.
* Add the above quantities and the number of original pints together.
* Perform the required multiplication to determine the number of pints.
* Convert the pints to gallons by dividing by 8.
* The quotient is the number of gallons and the remainder is the number of extra pints.
* Convert the extra pints to quarts by dividing the extra pints by 2.
* The quotient is the number of quarts and the remainder is the number of pints.
Example: Multiply 4 gallons 3 quarts and 1 pint times 5
* Convert 4 gallons to pints by multiplying 8 by 4:
8 * 4 = 32 pints
* Convert 3 quarts to pints by multiplying 3 by 2:
3 * 2 = 6 pints
* Add the pints from above and the number of original pints:
32 + 6 + 1 = 39 pints
* Perform the required multiplication:
39 * 5 = 195 pints
* Find the number of whole gallons by dividing by 8:
195 ÷ 8 = 24 R 3
* Find the number of whole quarts by dividing the remainder by 2:
3 ÷ 2 = 1 R 1
* The remainder of 1 is the number of pints.
* Answer: 24 gallons 1 quart and 1 pint
Dividing Gallons, Quarts and Pints
How to divide gallons, quarts and pints
* Convert gallons to pints by multiplying the number of gallons by 8.
* Convert quarts to pints by multiplying the number of quarts by 2.
* Add the above quantities and the number of original pints together.
* Perform the required division to determine the number of pints.
* Convert the pints to gallons by dividing by 8.
* The quotient is the number of gallons and the remainder is the number of extra pints.
* Convert the extra pints to quarts by dividing the extra pints by 2.
* The quotient is the number of quarts and the remainder is the number of pints.
Example: Divide 9 gallons 1 quart and 1 pint by 5.
* Convert 9 gallons to pints by multiplying 9 times 8:
9 * 8 = 72 pints
* Convert 1 quart to pints by multiplying 1 times 2:
1 * 2 = 2 pints
* Add the pints from above and the number of original pints:
72 + 2 + 1 = 75 pints
* Perform the required division:
75 ÷ 5 = 15 pints
* Find the number of whole gallons by dividing by 8:
15 ÷ 8 = 1 R 7
* Find the number of whole quarts by dividing the remainder by 2:
7 ÷ 2 = 3 R 1
* The remainder of 1 is the number of pints.
* Answer: 1 gallon 3 quarts and 1 pint
Dividing Gallons, Quarts and Pints
How to divide gallons, quarts and pints
* Convert gallons to pints by multiplying the number of gallons by 8.
* Convert quarts to pints by multiplying the number of quarts by 2.
* Add the above quantities and the number of original pints together.
* Perform the required division to determine the number of pints.
* Convert the pints to gallons by dividing by 8.
* The quotient is the number of gallons and the remainder is the number of extra pints.
* Convert the extra pints to quarts by dividing the extra pints by 2.
* The quotient is the number of quarts and the remainder is the number of pints.
Example: Divide 9 gallons 1 quart and 1 pint by 5.
* Convert 9 gallons to pints by multiplying 9 times 8:
9 * 8 = 72 pints
* Convert 1 quart to pints by multiplying 1 times 2:
1 * 2 = 2 pints
* Add the pints from above and the number of original pints:
72 + 2 + 1 = 75 pints
* Perform the required division:
75 ÷ 5 = 15 pints
* Find the number of whole gallons by dividing by 8:
15 ÷ 8 = 1 R 7
* Find the number of whole quarts by dividing the remainder by 2:
7 ÷ 2 = 3 R 1
* The remainder of 1 is the number of pints.
* Answer: 1 gallon 3 quarts and 1 pint
The metric system uses the Celsius scale to measure temperature. However, temperatures are still measured on the Fahrenheit scale in the U.S.
Water freezes at 0o Celsius and boils at 100o Celsius which is a difference of 100o. Water freezes at 32o Fahrenheit and boils at 212o Fahrenheit which is a difference of 180o. Therefore each degree on the Celsius scale is equal to 180/100 or 9/5 degrees on the Fahrenheit scale.
* How to convert Celsius temperatures to Fahrenheit Multiply the Celsius temperature by 9/5.
* Add 32o to adjust for the offset in the Fahrenheit scale.
* Example: convert 37o C to Fahrenheit.
37 * 9/5 = 333/5 = 66.6
66.6 + 32 = 98.6o F
There is a mental math method to convert from Celsius to Fahrenheit. The ratio of 9/5 is equal to 1.8 and 1.8 is equivalent to 2 - 0.2
* How to convert Celsius temperatures to Fahrenheit with mental math. Double the Celsius temperature (multiply by 2).
* Take 1/10 of this number (2 * 1/10 = 0.2) and subtract it from the number above.
* Add 32o to adjust for the offset in the Fahrenheit scale.
*
* Example: convert 37o C to Fahrenheit.
37 * 2 = 74
74 * 1/10 = 7.4
74 - 7.4 = 66.6
66.6 + 32 = 98.6o F
Temperature Conversion - Celsius to Fahrenheit
The metric system uses the Celsius scale to measure temperature. However, temperatures are still measured on the Fahrenheit scale in the U.S.
Water freezes at 0o Celsius and boils at 100o Celsius which is a difference of 100o. Water freezes at 32o Fahrenheit and boils at 212o Fahrenheit which is a difference of 180o. Therefore each degree on the Celsius scale is equal to 180/100 or 9/5 degrees on the Fahrenheit scale.
* How to convert Celsius temperatures to Fahrenheit Multiply the Celsius temperature by 9/5.
* Add 32o to adjust for the offset in the Fahrenheit scale.
* Example: convert 37o C to Fahrenheit.
37 * 9/5 = 333/5 = 66.6
66.6 + 32 = 98.6o F
There is a mental math method to convert from Celsius to Fahrenheit. The ratio of 9/5 is equal to 1.8 and 1.8 is equivalent to 2 - 0.2
* How to convert Celsius temperatures to Fahrenheit with mental math. Double the Celsius temperature (multiply by 2).
* Take 1/10 of this number (2 * 1/10 = 0.2) and subtract it from the number above.
* Add 32o to adjust for the offset in the Fahrenheit scale.
*
* Example: convert 37o C to Fahrenheit.
37 * 2 = 74
74 * 1/10 = 7.4
74 - 7.4 = 66.6
66.6 + 32 = 98.6o F
Note: This lesson includes temperatures that use negative numbers. Negative numbers follow a pattern that is opposite of positive numbers. The number -20 is smaller than the number -10. Example of counting with negative and positive numbers: -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5.
* Example of converting negative Celsius temperatures to Fahrenheit Convert -15o C to Fahrenheit.
* -15 * 9/5 = -135/5 = -27
* -27 + 32 = 5o F
Temperature Conversion - Fahrenheit to Celsius
The metric system uses the Celsius scale to measure temperature. However, temperatures are still measured on the Fahrenheit scale in the U.S.
Water freezes at 0o Celsius and boils at 100o Celsius which is a difference of 100o. Water freezes at 32o Fahrenheit and boils at 212o Fahrenheit which is a difference of 180o. Therefore each degree on the Fahrenheit scale is equal to 100/180 or 5/9 degrees on the Celsius scale.
* How to convert Fahrenheit temperatures to Celsius Subtract 32o to adjust for the offset in the Fahrenheit scale.
* Multiply the result by 5/9.
* Example: convert 98.6o Fahrenheit to Celsius.
98.6 - 32 = 66.6
66.6 * 5/9 = 333/9 = 37o C.
There is a mental math method to approximate the Fahrenheit to Celsius conversion. The ratio of 5/9 is approximately equal to 0.55555....
* How to approximate the conversion of Fahrenheit temperatures to Celsius with mental math. Subtract 32o to adjust for the offset in the Fahrenheit scale.
* Divide the Celsius temperature by 2 (multiply by 0.5).
* Take 1/10 of this number (0.5 * 1/10 = 0.05) and add it from the number above.
* Example: convert 98.6o F to Celsius.
98.6 - 32 = 66.6
66.6 * 1/2 = 33.3
33.3 * 1/10 = 3.3
33.3 + 3.3 = 36.6 which is an approximation of the Celsius temperature
Temperature Conversion - Fahrenheit to Celsius
The metric system uses the Celsius scale to measure temperature. However, temperatures are still measured on the Fahrenheit scale in the U.S.
Water freezes at 0o Celsius and boils at 100o Celsius which is a difference of 100o. Water freezes at 32o Fahrenheit and boils at 212o Fahrenheit which is a difference of 180o. Therefore each degree on the Fahrenheit scale is equal to 100/180 or 5/9 degrees on the Celsius scale.
* How to convert Fahrenheit temperatures to Celsius Subtract 32o to adjust for the offset in the Fahrenheit scale.
* Multiply the result by 5/9.
* Example: convert 98.6o Fahrenheit to Celsius.
98.6 - 32 = 66.6
66.6 * 5/9 = 333/9 = 37o C.
There is a mental math method to approximate the Fahrenheit to Celsius conversion. The ratio of 5/9 is approximately equal to 0.55555....
* How to approximate the conversion of Fahrenheit temperatures to Celsius with mental math. Subtract 32o to adjust for the offset in the Fahrenheit scale.
* Divide the Celsius temperature by 2 (multiply by 0.5).
* Take 1/10 of this number (0.5 * 1/10 = 0.05) and add it from the number above.
* Example: convert 98.6o F to Celsius.
98.6 - 32 = 66.6
66.6 * 1/2 = 33.3
33.3 * 1/10 = 3.3
33.3 + 3.3 = 36.6 which is an approximation of the Celsius temperature
Note: This lesson includes temperatures that use negative numbers. Negative numbers follow a pattern that is opposite of positive numbers. The number -20 is smaller than the number -10. Example of counting with negative and positive numbers: -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5
* Example of converting negative Fahrenheit temperatures to Celsius Convert -4o F to Celsius.
* -4 - 32 = -36
* -36 * 5/9 = -180/9 = -20o C
Converting between Metric Units of Mass
The metric system has prefix modifiers that are multiples of 10.
* A kilogram is 1000 grams
* A hectogram is 100 grams
* A decagram is 10 grams
* A gram is the stem unit of mass
* A decigram is 1/10 gram
* A centigram is 1/100 gram
* A milligram is 1/1000 gram
As we move down the units, the next unit is one tenth as heavy. As we move upward, each unit is 10 times as heavy. One hundred milligrams, which is 1/10 gram (100/1000=1/10) are heavier than one centigram (1/100th gram).
Comparing Mass in Grams
The metric system has prefix modifiers that are powers of 10.
* A kilogram is 1000 grams
* A hectogram is 100 grams
* A decagram is 10 grams
* A gram is the basic unit of mass
* A decigram is 1/10 gram
* A centigram is 1/100 gram
* A milligram is 1/1000 gram
Multiplying Pounds and Ounces
How to multiply pounds and ounces
* Convert pounds and ounces to ounces by multiplying pounds by 16 and adding the number of ounces
* Perform the required multiplication to determine the number of ounces.
* Convert the ounces to pounds and ounces by dividing by 16.
* The quotient is the number of pounds and the remainder is the number of ounces.
Example: Multiply 5 pounds 6 ounces times 4
* Convert 5 pounds to ounces by multiplying 16 by 5:
16 * 5 = 80 ounces
* Add the number of extra ounces:
80 + 6 = 86 ounces
* Perform the required multiplication:
86 * 4 = 344 ounces
* Convert to pounds and ounces by dividing by 16:
344 ÷ 16 = 21 R 8
* The quotient (21) is the number of pounds and the remainder (8) is the number of ounces.
* Answer: 21 pounds 8 ounces
Dividing Pounds and Ounces
How to divide pounds and ounces
* Convert pounds and ounces to ounces by multiplying pounds by 16 and adding the number of ounces
* Perform the required division to determine the number of ounces.
* Convert the ounces to pounds and ounces by dividing by 16.
* The quotient is the number of pounds and the remainder is the number of ounces.
Example: Divide 10 pounds 0 ounces by 4
* Convert 10 pounds to ounces by multiplying 10 by 16:
16 * 10 = 160 ounces
* Add the number of extra ounces:
160 + 0 = 160 ounces
* Perform the required division:
160 ÷ 4 = 40 ounces
* Convert to pounds and ounces by dividing by 16:
40 ÷ 16 = 2 R 8
* The quotient (2) is the number of pounds and the remainder (8) is the number of ounces.
* Answer: 2 pounds 8 ounces
Converting Metric Volume Units
The metric system has prefix modifiers that are multiples of 10.
* A kiloliter is 1000 liters
* A hectoliter is 100 liters
* A decaliter is 10 liters
* A liter is the basic unit of volume
* A deciliter is 1/10 liter
* A centiliter is 1/100 liter
* A milliliter is 1/1000 liter
As we move down the units, the next unit is one tenth as large. As we move upward, each unit is 10 times as large. One hundred milliliters, which is 1/10 liter (100/1000=1/10) are larger than one centiliter (1/100th liter).
Comparing Metric Liters
The metric system has prefix modifiers that are powers of 10.
* A kiloliter is 1000 liters
* A hectoliter is 100 liters
* A decaliter is 10 liters
* A liter is the basic unit of volume
* A deciliter is 1/10 liter
* A centiliter is 1/100 liter
* A milliliter is 1/1000 liter
Comparing Volume by Metric Prefixes
The metric system uses prefixes to indicate the size of the units of measurement. Each prefix varies from the next by a factor of ten. It is either ten times as large or one tenth the size.
The common prefixes with their values are:
* kilo = 1000
* hecto = 100
* deca = 10
* no prefix = 1
* deci = 1/10
* centi = 1/100
* milli = 1/1000
An example of comparing volume based on metric prefixes is: A deciliter is larger than a milliliter.
Multiplying Gallons, Quarts and Pints
How to multiply gallons, quarts and pints
* Convert gallons to pints by multiplying the number of gallons by 8.
* Convert quarts to pints by multiplying the number of quarts by 2.
* Add the above quantities and the number of original pints together.
* Perform the required multiplication to determine the number of pints.
* Convert the pints to gallons by dividing by 8.
* The quotient is the number of gallons and the remainder is the number of extra pints.
* Convert the extra pints to quarts by dividing the extra pints by 2.
* The quotient is the number of quarts and the remainder is the number of pints.
Example: Multiply 4 gallons 3 quarts and 1 pint times 5
* Convert 4 gallons to pints by multiplying 8 by 4:
8 * 4 = 32 pints
* Convert 3 quarts to pints by multiplying 3 by 2:
3 * 2 = 6 pints
* Add the pints from above and the number of original pints:
32 + 6 + 1 = 39 pints
* Perform the required multiplication:
39 * 5 = 195 pints
* Find the number of whole gallons by dividing by 8:
195 ÷ 8 = 24 R 3
* Find the number of whole quarts by dividing the remainder by 2:
3 ÷ 2 = 1 R 1
* The remainder of 1 is the number of pints.
* Answer: 24 gallons 1 quart and 1 pint
Dividing Gallons, Quarts and Pints
How to divide gallons, quarts and pints
* Convert gallons to pints by multiplying the number of gallons by 8.
* Convert quarts to pints by multiplying the number of quarts by 2.
* Add the above quantities and the number of original pints together.
* Perform the required division to determine the number of pints.
* Convert the pints to gallons by dividing by 8.
* The quotient is the number of gallons and the remainder is the number of extra pints.
* Convert the extra pints to quarts by dividing the extra pints by 2.
* The quotient is the number of quarts and the remainder is the number of pints.
Example: Divide 9 gallons 1 quart and 1 pint by 5.
* Convert 9 gallons to pints by multiplying 9 times 8:
9 * 8 = 72 pints
* Convert 1 quart to pints by multiplying 1 times 2:
1 * 2 = 2 pints
* Add the pints from above and the number of original pints:
72 + 2 + 1 = 75 pints
* Perform the required division:
75 ÷ 5 = 15 pints
* Find the number of whole gallons by dividing by 8:
15 ÷ 8 = 1 R 7
* Find the number of whole quarts by dividing the remainder by 2:
7 ÷ 2 = 3 R 1
* The remainder of 1 is the number of pints.
* Answer: 1 gallon 3 quarts and 1 pint
Dividing Gallons, Quarts and Pints
How to divide gallons, quarts and pints
* Convert gallons to pints by multiplying the number of gallons by 8.
* Convert quarts to pints by multiplying the number of quarts by 2.
* Add the above quantities and the number of original pints together.
* Perform the required division to determine the number of pints.
* Convert the pints to gallons by dividing by 8.
* The quotient is the number of gallons and the remainder is the number of extra pints.
* Convert the extra pints to quarts by dividing the extra pints by 2.
* The quotient is the number of quarts and the remainder is the number of pints.
Example: Divide 9 gallons 1 quart and 1 pint by 5.
* Convert 9 gallons to pints by multiplying 9 times 8:
9 * 8 = 72 pints
* Convert 1 quart to pints by multiplying 1 times 2:
1 * 2 = 2 pints
* Add the pints from above and the number of original pints:
72 + 2 + 1 = 75 pints
* Perform the required division:
75 ÷ 5 = 15 pints
* Find the number of whole gallons by dividing by 8:
15 ÷ 8 = 1 R 7
* Find the number of whole quarts by dividing the remainder by 2:
7 ÷ 2 = 3 R 1
* The remainder of 1 is the number of pints.
* Answer: 1 gallon 3 quarts and 1 pint
Properties, Special Quantities and Operations
Factors
A number may be made by multiplying two or more other numbers together. The numbers that are multiplied together are called factors of the final number. All numbers have a factor of one since one multiplied by any number equals that number. All numbers can be divided by themselves to produce the number one. Therefore, we normally ignore one and the number itself as useful factors.
The number fifteen can be divided into two factors which are three and five.
The number twelve could be divided into two factors which are 6 and 2. Six could be divided into two further factors of 2 and 3. Therefore the factors of twelve are 2, 2, and 3.
If twelve was first divided into the factors 3 and 4, the four could be divided into factors of 2 and 2. Therefore the factors of twelve are still 2, 2, and 3.
* There are several clues to help determine factors. Any even number has a factor of two
* Any number ending in 5 has a factor of five
* Any number above 0 that ends with 0 (such as 10, 30, 1200) has factors of two and five.
To determine factors see if one of the above rules apply (ends in 5, 0 or an even number). If none of the rules apply, there still may be factors of 3 or 7 or some other number.
Prime and Composite Numbers
A prime number is a whole number that only has two factors which are itself and one. A composite number has factors in addition to one and itself.
The numbers 0 and 1 are neither prime nor composite.
All even numbers are divisible by two and so all even numbers greater than two are composite numbers.
All numbers that end in five are divisible by five. Therefore all numbers that end with five and are greater than five are composite numbers.
The prime numbers between 2 and 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.
Greatest Common Factor
The Greatest Common Factor (GCF) is the largest number that is a common factor of two or more numbers.
How to find the greatest common factor:
* Determine if there is a common factor of the numbers. A common factor is a number that will divide into both numbers evenly. Two is a common factor of 4 and 14.
* Divide all of the numbers by this common factor.
* Repeat this process with the resulting numbers until there are no more common factors.
* Multiply all of the common factors together to find the Greatest Common Factor
Simplifying Fractions
Fractions may have numerators and denominators that are composite numbers (numbers that has more factors than 1 and itself).
How to simplify a fraction:
* Find a common factor of the numerator and denominator. A common factor is a number that will divide into both numbers evenly. Two is a common factor of 4 and 14.
* Divide both the numerator and denominator by the common factor.
* Repeat this process until there are no more common factors.
* The fraction is simplified when no more common factors exist.
Another method to simplify a fraction
* Find the Greatest Common Factor (GCF) of the numerator and denominator
* Divide the numerator and the denominator by the GCF
Least Common Multiple
The Least Common Multiple (LCM) is the smallest number that two or more numbers will divide into evenly.
How to find the Least Common Multiple of two numbers:
* Find the Greatest Common Factor (GCF) of the numbers
* Multiply the numbers together
* Divide the product of the numbers by the GCF.
Example: Find the LCM of 15 and 12
* Determine the Greatest Common Factor of 15 and 12 which is 3
* Either multiply the numbers and divide by the GCF (15*12=180, 180/3=60)
* OR - Divide one of the numbers by the GCF and multiply the answer times the other number (15/3=5, 5*12=60)
Least Common Denominator
The Least Common Denominator (LCD) is the Least Common Multiple of two or more denominators.
How to find the Least Common Denominator:
* Find the Greatest Common Factor of the denominators.
* Multiply the denominators together.
* Divide the product of the denominators by the Greatest Common Factor.
Example: Find the LCD of 2/9 and 3/12
* Determine the Greatest Common Factor of 9 and 12 which is 3
* Either multiply the denominators and divide by the GCF (9*12=108, 108/3=36)
* OR - Divide one of the denominators by the GCF and multiply the quotient times the other denominator (9/3=3, 3*12=36)
How to rename fractions and use the Least Common Denominator:
* Divide the LCD by one denominator.
* Multiply the numerator times this quotient.
* Repeat the process for the other fraction(s)
Example: Add 2/9 + 3/12
* LCD is 36
* First fraction (2/9): 36/9 = 4, 4*2 = 8, first fraction is renamed as 8/36
* Second fraction (3/12): 36/12 = 3, 3*3 = 9, second fraction is renamed as 9/36
* It is possible to add or subtract fractions that have the same denominator
* 8/36 + 9/36 = 17/36
Estimating by Front End Estimation
Front end estimation mostly produces a closer estimate of sums or differences than the answer produced by adding or subtracting rounded numbers.
How to estimate a sum by front end estimation:
* Add the digits of the two highest place values
* Insert zeros for the other place values
* Example 1: 4496 + 3745 is estimated to be 8100 by front end estimation (i.e. 4400 + 3700).
* Example 2: 4496 + 745 is estimated to be 5100 by front end estimation (i.e. 4400 + 700).
Estimating by front end estimation
Front end estimation generally produces a better estimate of sums or differences than rounding before adding or subtracting.
How to estimate a difference by front end estimation:
* Subtract the digits of the two highest place values
* Insert zeros for the other place values
*
* Example: 7396 minus 3745 is estimated to be 3600 by front end estimation (i.e. 7300-3700).
Calculations using the Order of Operations
The order of operations are rules that govern which mathematical operations are done first.
* Do operations in parentheses and other grouping symbols first. If there are grouping symbols within other grouping symbols do the innermost first.
* Do multiplication and division operations from left to right.
* Do addition and subtraction operations from left to right
Example: 2+3*(4+(6*3-8))*2
2+3*(4+(18-8))*2
2+3*(4+10)*2
2+3*14*2
2+42*2
2+84
86
Properties of Addition
There are four mathematical properties which involve addition. The properties are the commutative, associative, additive identity and distributive properties.
Commutative property: When two numbers are added, the sum is the same regardless of the order of the addends. For example 4 + 2 = 2 + 4
Associative Property: When three or more numbers are added, the sum is the same regardless of the grouping of the addends. For example (2 + 3) + 4 = 2 + (3 + 4)
Additive Identity Property: The sum of any number and zero is the original number. For example 5 + 0 = 5.
Distributive property: The sum of two numbers times a third number is equal to the sum of each addend times the third number. For example 4 * (6 + 3) = 4*6 + 4*3
Multiplication Properties
There are four properties involving multiplication that will help make problems easier to solve. They are the commutative, associative, multiplicative identity and distributive properties.
Commutative property: When two numbers are multiplied together, the product is the same regardless of the order of the multiplicands. For example 4 * 2 = 2 * 4
Associative Property: When three or more numbers are multiplied, the product is the same regardless of the grouping of the factors. For example (2 * 3) * 4 = 2 * (3 * 4)
Multiplicative Identity Property: The product of any number and one is that number. For example 5 * 1 = 5.
Distributive property: The sum of two numbers times a third number is equal to the sum of each addend times the third number. For example 4 * (6 + 3) = 4*6 + 4*3
A number may be made by multiplying two or more other numbers together. The numbers that are multiplied together are called factors of the final number. All numbers have a factor of one since one multiplied by any number equals that number. All numbers can be divided by themselves to produce the number one. Therefore, we normally ignore one and the number itself as useful factors.
The number fifteen can be divided into two factors which are three and five.
The number twelve could be divided into two factors which are 6 and 2. Six could be divided into two further factors of 2 and 3. Therefore the factors of twelve are 2, 2, and 3.
If twelve was first divided into the factors 3 and 4, the four could be divided into factors of 2 and 2. Therefore the factors of twelve are still 2, 2, and 3.
* There are several clues to help determine factors. Any even number has a factor of two
* Any number ending in 5 has a factor of five
* Any number above 0 that ends with 0 (such as 10, 30, 1200) has factors of two and five.
To determine factors see if one of the above rules apply (ends in 5, 0 or an even number). If none of the rules apply, there still may be factors of 3 or 7 or some other number.
Prime and Composite Numbers
A prime number is a whole number that only has two factors which are itself and one. A composite number has factors in addition to one and itself.
The numbers 0 and 1 are neither prime nor composite.
All even numbers are divisible by two and so all even numbers greater than two are composite numbers.
All numbers that end in five are divisible by five. Therefore all numbers that end with five and are greater than five are composite numbers.
The prime numbers between 2 and 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.
Greatest Common Factor
The Greatest Common Factor (GCF) is the largest number that is a common factor of two or more numbers.
How to find the greatest common factor:
* Determine if there is a common factor of the numbers. A common factor is a number that will divide into both numbers evenly. Two is a common factor of 4 and 14.
* Divide all of the numbers by this common factor.
* Repeat this process with the resulting numbers until there are no more common factors.
* Multiply all of the common factors together to find the Greatest Common Factor
Simplifying Fractions
Fractions may have numerators and denominators that are composite numbers (numbers that has more factors than 1 and itself).
How to simplify a fraction:
* Find a common factor of the numerator and denominator. A common factor is a number that will divide into both numbers evenly. Two is a common factor of 4 and 14.
* Divide both the numerator and denominator by the common factor.
* Repeat this process until there are no more common factors.
* The fraction is simplified when no more common factors exist.
Another method to simplify a fraction
* Find the Greatest Common Factor (GCF) of the numerator and denominator
* Divide the numerator and the denominator by the GCF
Least Common Multiple
The Least Common Multiple (LCM) is the smallest number that two or more numbers will divide into evenly.
How to find the Least Common Multiple of two numbers:
* Find the Greatest Common Factor (GCF) of the numbers
* Multiply the numbers together
* Divide the product of the numbers by the GCF.
Example: Find the LCM of 15 and 12
* Determine the Greatest Common Factor of 15 and 12 which is 3
* Either multiply the numbers and divide by the GCF (15*12=180, 180/3=60)
* OR - Divide one of the numbers by the GCF and multiply the answer times the other number (15/3=5, 5*12=60)
Least Common Denominator
The Least Common Denominator (LCD) is the Least Common Multiple of two or more denominators.
How to find the Least Common Denominator:
* Find the Greatest Common Factor of the denominators.
* Multiply the denominators together.
* Divide the product of the denominators by the Greatest Common Factor.
Example: Find the LCD of 2/9 and 3/12
* Determine the Greatest Common Factor of 9 and 12 which is 3
* Either multiply the denominators and divide by the GCF (9*12=108, 108/3=36)
* OR - Divide one of the denominators by the GCF and multiply the quotient times the other denominator (9/3=3, 3*12=36)
How to rename fractions and use the Least Common Denominator:
* Divide the LCD by one denominator.
* Multiply the numerator times this quotient.
* Repeat the process for the other fraction(s)
Example: Add 2/9 + 3/12
* LCD is 36
* First fraction (2/9): 36/9 = 4, 4*2 = 8, first fraction is renamed as 8/36
* Second fraction (3/12): 36/12 = 3, 3*3 = 9, second fraction is renamed as 9/36
* It is possible to add or subtract fractions that have the same denominator
* 8/36 + 9/36 = 17/36
Estimating by Front End Estimation
Front end estimation mostly produces a closer estimate of sums or differences than the answer produced by adding or subtracting rounded numbers.
How to estimate a sum by front end estimation:
* Add the digits of the two highest place values
* Insert zeros for the other place values
* Example 1: 4496 + 3745 is estimated to be 8100 by front end estimation (i.e. 4400 + 3700).
* Example 2: 4496 + 745 is estimated to be 5100 by front end estimation (i.e. 4400 + 700).
Estimating by front end estimation
Front end estimation generally produces a better estimate of sums or differences than rounding before adding or subtracting.
How to estimate a difference by front end estimation:
* Subtract the digits of the two highest place values
* Insert zeros for the other place values
*
* Example: 7396 minus 3745 is estimated to be 3600 by front end estimation (i.e. 7300-3700).
Calculations using the Order of Operations
The order of operations are rules that govern which mathematical operations are done first.
* Do operations in parentheses and other grouping symbols first. If there are grouping symbols within other grouping symbols do the innermost first.
* Do multiplication and division operations from left to right.
* Do addition and subtraction operations from left to right
Example: 2+3*(4+(6*3-8))*2
2+3*(4+(18-8))*2
2+3*(4+10)*2
2+3*14*2
2+42*2
2+84
86
Properties of Addition
There are four mathematical properties which involve addition. The properties are the commutative, associative, additive identity and distributive properties.
Commutative property: When two numbers are added, the sum is the same regardless of the order of the addends. For example 4 + 2 = 2 + 4
Associative Property: When three or more numbers are added, the sum is the same regardless of the grouping of the addends. For example (2 + 3) + 4 = 2 + (3 + 4)
Additive Identity Property: The sum of any number and zero is the original number. For example 5 + 0 = 5.
Distributive property: The sum of two numbers times a third number is equal to the sum of each addend times the third number. For example 4 * (6 + 3) = 4*6 + 4*3
Multiplication Properties
There are four properties involving multiplication that will help make problems easier to solve. They are the commutative, associative, multiplicative identity and distributive properties.
Commutative property: When two numbers are multiplied together, the product is the same regardless of the order of the multiplicands. For example 4 * 2 = 2 * 4
Associative Property: When three or more numbers are multiplied, the product is the same regardless of the grouping of the factors. For example (2 * 3) * 4 = 2 * (3 * 4)
Multiplicative Identity Property: The product of any number and one is that number. For example 5 * 1 = 5.
Distributive property: The sum of two numbers times a third number is equal to the sum of each addend times the third number. For example 4 * (6 + 3) = 4*6 + 4*3
Monday, November 3, 2008
Divisibility
Numbers Divisible by 3
Numbers are divisible by 3 if the sum of all the individual digits is evenly divisible by 3. For example, the sum of the digits for the number 3627 is 18, which is evenly divisible by 3 so the number 3627 is evenly divisible by 3.
Numbers Divisible by 4
Whole numbers are divisible by 4 if the number formed by the last two individual digits is evenly divisible by 4. For example, the number formed by the last two digits of the number 3628 is 28, which is evenly divisible by 4 so the number 3628 is evenly divisible by 4.
Why is this always true?
Numbers Divisible by 5
Numbers are evenly divisible by 5 if the last digit of the number is 0 or 5.
Numbers Divisible by 6
Numbers are evenly divisible by 6 if they are evenly divisible by both 2 AND 3. Even numbers are always evenly divisible by 2. Numbers are evenly divisible by 3 if the sum of all the individual digits is evenly divisible by 3. For example, the sum of the digits for the number 3627 is 18, which is evenly divisible by 3 but 3627 is an odd number so the number 3627 is not evenly divisible by 6.
Numbers Divisible by 7
To determine if a number is divisible by 7, take the last digit off the number, double it and subtract the doubled number from the remaining number. If the result is evenly divisible by 7 (e.g. 14, 7, 0, -7, etc.), then the number is divisible by seven. This may need to be repeated several times.
Example: Is 3101 evenly divisible by 7?
310 - take off the last digit of the number which was 1
-2 - double the removed digit and subtract it
308 - repeat the process by taking off the 8
-16 - and doubling it to get 16 which is subtracted
14 - the result is 14 which is a multiple of 7
Numbers Divisible by 8
Numbers are divisible by 8 if the number formed by the last three individual digits is evenly divisible by 8. For example, the last three digits of the number 3624 is 624, which is evenly divisible by 8 so 3624 is evenly divisible by 8.
Numbers Divisible by 9
A number is divisible by 10 only if the last digit is a 0. Numbers are divisible by 9 if the sum of all the individual digits is evenly divisible by 9. For example, the last sum of the digits of the number 3627 is 18, which is evenly divisible by 9 so 3627 is evenly divisible by 9.
Ratios
Ratios
Ratios tell how one number is related to another number.
A ratio may be written as A:B or A/B or by the phrase "A to B".
A ratio of 1:5 says that the second number is five times as large as the first.
The following steps will allow determination of a number when one number and the ratio between the numbers is given.
Example: Determine the value of B if A=6 and the ratio of A:B = 2:5
* Determine how many times the number A is divisible by the corresponding portion of the ratio. (6/2=3)
* Multiply this number by the portion of the ratio representing B (3*5=15)
* Therefore if the ratio of A:B is 2:5 and A=6 then B=15
How to Determine a Ratio
Ratios represent how one quantity is related to another quantity.
A ratio may be written as A:B or A/B or by the phrase "A to B".
A ratio of 1:5 says that the second quantity is five times as large as the first.
The following steps will allow a ratio to be determination if two numbers are known.
Example: Determine the ratio of 24 to 40.
* Divide both terms of the ratio by the greatest common factor (24/8 = 3, 40/8=5)
* State the ratio. (The ratio of 24 to 40 is 3:5)
Cross multiplication to solve proportions
A proportion is an equation which states that two ratios are equal.
When the terms of a proportion are cross multiplied, the cross products are equal.
Cross multiplication is the multiplication of the numerator of the first ratio by the denominator of the second ratio and the multiplication of the denominator of the first ratio by the numerator of the second ratio.
21 3
-- = --
70 10
21 * 10 = 70 * 3
210 = 210
If one term of a proportion is not known, cross multiplication can be used to find the value of that term.
x 3
-- = --
70 10
x * 10 = 70 * 3
10x = 210
10x 210
--- = ---
10 10
x = 21
Unit Rates
A rate is a ratio that is used to compare different kinds of quantities.
A unit rate describes how many units of the first type of quantity corresponds to one unit of the second type of quantity.
Some common unit rates are miles (or kilometers) per hour, cost per item, earnings per week, etc. In each case the first quantity is related to 1 unit of the second quantity.
Ratios tell how one number is related to another number.
A ratio may be written as A:B or A/B or by the phrase "A to B".
A ratio of 1:5 says that the second number is five times as large as the first.
The following steps will allow determination of a number when one number and the ratio between the numbers is given.
Example: Determine the value of B if A=6 and the ratio of A:B = 2:5
* Determine how many times the number A is divisible by the corresponding portion of the ratio. (6/2=3)
* Multiply this number by the portion of the ratio representing B (3*5=15)
* Therefore if the ratio of A:B is 2:5 and A=6 then B=15
How to Determine a Ratio
Ratios represent how one quantity is related to another quantity.
A ratio may be written as A:B or A/B or by the phrase "A to B".
A ratio of 1:5 says that the second quantity is five times as large as the first.
The following steps will allow a ratio to be determination if two numbers are known.
Example: Determine the ratio of 24 to 40.
* Divide both terms of the ratio by the greatest common factor (24/8 = 3, 40/8=5)
* State the ratio. (The ratio of 24 to 40 is 3:5)
Cross multiplication to solve proportions
A proportion is an equation which states that two ratios are equal.
When the terms of a proportion are cross multiplied, the cross products are equal.
Cross multiplication is the multiplication of the numerator of the first ratio by the denominator of the second ratio and the multiplication of the denominator of the first ratio by the numerator of the second ratio.
21 3
-- = --
70 10
21 * 10 = 70 * 3
210 = 210
If one term of a proportion is not known, cross multiplication can be used to find the value of that term.
x 3
-- = --
70 10
x * 10 = 70 * 3
10x = 210
10x 210
--- = ---
10 10
x = 21
Unit Rates
A rate is a ratio that is used to compare different kinds of quantities.
A unit rate describes how many units of the first type of quantity corresponds to one unit of the second type of quantity.
Some common unit rates are miles (or kilometers) per hour, cost per item, earnings per week, etc. In each case the first quantity is related to 1 unit of the second quantity.
Computation with Fractions and Decimals
Multiplying Thousandths by Thousandths
Multiplying two three digit decimals is very similar to the previous procedures. The following explanation will not go step by step but will only show the work that would be done.
* Place one decimal above the other so that they are lined up on the right side. Draw a line under the bottom number. Temporarily disregard the decimal points and multiply the numbers like you would multiply a three digit number by a three digit number.
0.529
0.467
3703
3174
2116
0.247043
* At the start we disregarded the decimal points. In the answer we counted up the decimal places and moved the decimal place to its proper location. We have three decimal places in both numbers so we move the decimal six places to the left to give the final answer of 0.247043.
Division of Decimals by Whole Numbers
The procedure for the division of decimals is very similar to the division of whole numbers.
How to divide a four digit decimal number by a two digit number (e.g. 0.4131 ÷ 17).
* Place the divisor (17) before the division bracket and place the dividend (0.4131) under it.
17)0.4131
* Proceed with the division as you normally would except put the decimal point in the answer or quotient exactly above where it occurs in the dividend. For example:
0.0243
17)0.4131
Adding Fractions with Different Denominators
How to Add Fractions with different denominators:
* Find the Least Common Denominator (LCD) of the fractions
* Rename the fractions to have the LCD
* Add the numerators of the fractions
* Simplify the Fraction
Example: Find the Sum of 2/9 and 3/12
* Determine the Greatest Common Factor of 9 and 12 which is 3
* Either multiply the denominators and divide by the GCF (9*12=108, 108/3=36)
* OR - Divide one of the denominators by the GCF and multiply the answer by the other denominator (9/3=3, 3*12=36)
* Rename the fractions to use the Least Common Denominator(2/9=8/36, 3/12=9/36)
* The result is 8/36 + 9/36
* Add the numerators and put the sum over the LCD = 17/36
* Simplify the fraction if possible. In this case it is not possible
Multiplying Fractions
To Multiply Fractions:
* Multiply the numerators of the fractions
* Multiply the denominators of the fractions
* Place the product of the numerators over the product of the denominators
* Simplify the Fraction
Example: Multiply 2/9 and 3/12
* Multiply the numerators (2*3=6)
* Multiply the denominators (9*12=108)
* Place the product of the numerators over the product of the denominators (6/108)
* Simplify the Fraction (6/108 = 1/18)
*
* The Easy Way. It is often simplest to "cancel" before doing the multiplication. Canceling is dividing one factor of the numerator and one factor of the denominator by the same number.
* For example: 2/9 * 3/12 = (2*3)/(9*12) = (1*3)/(9*6) = (1*1)/(3*6) = 1/18
Multiplying Fractions by Whole Numbers
* Multiplying a fraction by an integer follows the same rules as multiplying two fractions.
* An integer can be considered to be a fraction with a denominator of 1.
* Therefore when a fraction is multiplied by an integer the numerator of the fraction is multiplied by the integer.
* The denominator is multiplied by 1 which does not change the denominator.
Dividing Fractions by Whole Numbers
To Divide Fractions by Whole Numbers:
* Treat the integer as a fraction (i.e. place it over the denominator 1)
* Invert (i.e. turn over) the denominator fraction and multiply the fractions
* Multiply the numerators of the fractions
* Multiply the denominators of the fractions
* Place the product of the numerators over the product of the denominators
* Simplify the Fraction
Example: Divide 2/9 by 2
* The integer divisor (2) can be considered to be a fraction (2/1)
* Invert the denominator fraction and multiply (2/9 ÷ 2/1 = 2/9 * 1/2)
* Multiply the numerators (2*1=2)
* Multiply the denominators (9*2=18)
* Place the product of the numerators over the product of the denominators (2/18)
* Simplify the Fraction if possible (2/18 = 1/9)
*
* The Easy Way. After inverting, it is often simplest to "cancel" before doing the multiplication. Canceling is dividing one factor of the numerator and one factor of the denominator by the same number.
* For example: 2/9 ÷ 2 = 2/9 ÷ 2/1 = 2/9*1/2 = (2*1)/(9*2) = (1*1)/(9*1) = 1/9
Dividing Fractions by Fractions
To Divide Fractions:
* Invert (i.e. turn over) the denominator fraction and multiply the fractions
* Multiply the numerators of the fractions
* Multiply the denominators of the fractions
* Place the product of the numerators over the product of the denominators
* Simplify the Fraction
Example: Divide 2/9 and 3/12
* Invert the denominator fraction and multiply (2/9 ÷ 3/12 = 2/9 * 12/3)
* Multiply the numerators (2*12=24)
* Multiply the denominators (9*3=27)
* Place the product of the numerators over the product of the denominators (24/27)
* Simplify the Fraction (24/27 = 8/9)
*
* The Easy Way. After inverting, it is often simplest to "cancel" before doing the multiplication. Canceling is dividing one factor of the numerator and one factor of the denominator by the same number.
* For example: 2/9 ÷ 3/12 = 2/9*12/3 = (2*12)/(9*3) = (2*4)/(3*3) = 8/9
Adding decimals
How to add Decimals that have different numbers of decimal places
* Write one number below the other so that the bottom decimal point is directly below and lined up with the top decimal point.
* Add each column starting at the right side.
Example: Add 3.2756 + 11.48
3.2756
11.48
14.7556
How to add three or more decimal numbers that have different numbers of decimal places.
* Write the numbers in a column so the decimal points are directly lined up.
* Add each column starting at the right side.
Example: Add 23.143 + 3.2756 + 11.48
23.143
3.2756
11.48
37.8986
Division of Decimals by Decimals
The procedure for the division of decimals is very similar to the division of whole numbers. Make the divisor into a whole number by multiplying both it and the dividend by the same number (such as 10, 100, 1000 etc.). An easy way to do this is to move the decimal point to the right end of the divisor and move the decimal point of the dividend the same number of places.
How to divide a four digit decimal number by a two digit decimal number (e.g 0.4131 ÷ 0.17).
* Place the divisor before the division bracket and place the dividend (0.4131) under it.
0.17)0.4131
* Multiply both the divisor and dividend by 100 so that the divisor is not a decimal but a whole number. In other words move the decimal point two places to the right in both the divisor and dividend
17)41.31
* Proceed with the division as you normally would except put the decimal point in the answer or quotient exactly above where it occurs in the dividend. For example:
2.43
17)41.31
Division of Decimals by Decimals
The procedure for the division of decimals is very similar to the division of whole numbers. Make the divisor into a whole number by multiplying both it and the dividend by the same number (such as 10, 100, 1000 etc.). An easy way to do this is to move the decimal point to the right end of the divisor and move the decimal point of the dividend the same number of places.
How to divide a four digit decimal number by a two digit decimal number (e.g. 0.424 ÷ 0.8).
* Place the divisor before the division bracket and place the dividend (0.424) under it.
0.8)0.424
* Multiply both the divisor and dividend by 10 so that the divisor is not a decimal but a whole number. In other words move the decimal point one place to the right in both the divisor and dividend
8)4.24
* Proceed with the division as you normally would except put the decimal point in the answer or quotient exactly above where it occurs in the dividend. For example:
0.53
8)4.24
4 0
24
0
Ordering Decimal Numbers
Numbers have an order or arrangement. The number two is between one and three. Three or more numbers can be placed in order. A number may come before the other numbers or it may come between them or after them.
Example: If we start with the numbers 4.3 and 8.78, the number 5.2764 would come between them, the number 9.1 would come after them and the number 2 would come before both of them.
Example: If we start with the numbers 4.3 and 4.78, the number 4.2764 would come before both of them, the number 4.9 would come after them and the number 4.5232 would come between them.
The order may be ascending (getting larger in value) or descending (becoming smaller in value).
Rounding Decimals
27.17469 rounded to the nearest whole number is 27
36.74691 rounded to the nearest whole number is 37
12.34690 rounded to the nearest tenth is 12.3
89.46917 rounded to the nearest tenth is 89.5
50.02139 rounded to the nearest hundredth is 50.02
72.63539 rounded to the nearest hundredth is 72.64
46.83531 rounded to the nearest thousandth is 46.835
9.63967 rounded to the nearest thousandth is 9.640
Rules for rounding decimals.
1. Retain the correct number of decimal places (e.g. 3 for thousandths, 0 for whole numbers)
2. If the next decimal place value is 5 or more, increase the value in the last retained decimal place by 1.
Estimate the difference between two decimals
How to Estimate a difference by rounding.
* Round each decimal term that will be subtracted.
* Subtract the rounded terms
Example: Estimate the difference of 0.988 - 0.53
* Round 0.988 - 0.53 to 1 - 0.5
* Subtract the rounded numbers to obtain the estimated difference of 0.5
* The actual difference of 0.988 - 0.53 is 0.458
Some uses of rounding are:
* Checking to see if you have enough money to buy what you want.
* Getting a rough idea of the correct answer to a problem
Estimate the sum of two decimals
How to Estimate a sum by rounding.
* Round each decimal term that will be added.
* Add the rounded terms
Example: Estimate the sum of 0.988 + 0.53
* Round 0.988 + 0.53 to 1 + 0.5
* Add the rounded numbers to obtain the estimated sum of 1.5
* The actual sum of 0.988 + 0.53 is 1.518
Some uses of rounding are:
* Checking to see if you have enough money to buy what you want.
* Getting a rough idea of the correct answer to a problem
Reciprocals
The product of a number and its reciprocal equals 1.
The reciprocal of 4 is 1/4.
The reciprocal of 2/3 is 3/2.
The reciprocal of 1 is 1.
The number 0 does not have a reciprocal because the product of any number and 0 equals 0.
Multiplying Mixed Numbers
Mixed numbers consist of an integer followed by a fraction.
* Multiplying two mixed numbers: Convert each mixed number to an improper fraction.
* Multiply the two numerators together.
* Multiply the two denominators together.
* Convert the result back to a mixed number if it is an improper fraction.
* Simplify the mixed number.
Example: 6 2/8 * 3 5/9 =

Multiplying two three digit decimals is very similar to the previous procedures. The following explanation will not go step by step but will only show the work that would be done.
* Place one decimal above the other so that they are lined up on the right side. Draw a line under the bottom number. Temporarily disregard the decimal points and multiply the numbers like you would multiply a three digit number by a three digit number.
0.529
0.467
3703
3174
2116
0.247043
* At the start we disregarded the decimal points. In the answer we counted up the decimal places and moved the decimal place to its proper location. We have three decimal places in both numbers so we move the decimal six places to the left to give the final answer of 0.247043.
Division of Decimals by Whole Numbers
The procedure for the division of decimals is very similar to the division of whole numbers.
How to divide a four digit decimal number by a two digit number (e.g. 0.4131 ÷ 17).
* Place the divisor (17) before the division bracket and place the dividend (0.4131) under it.
17)0.4131
* Proceed with the division as you normally would except put the decimal point in the answer or quotient exactly above where it occurs in the dividend. For example:
0.0243
17)0.4131
Adding Fractions with Different Denominators
How to Add Fractions with different denominators:
* Find the Least Common Denominator (LCD) of the fractions
* Rename the fractions to have the LCD
* Add the numerators of the fractions
* Simplify the Fraction
Example: Find the Sum of 2/9 and 3/12
* Determine the Greatest Common Factor of 9 and 12 which is 3
* Either multiply the denominators and divide by the GCF (9*12=108, 108/3=36)
* OR - Divide one of the denominators by the GCF and multiply the answer by the other denominator (9/3=3, 3*12=36)
* Rename the fractions to use the Least Common Denominator(2/9=8/36, 3/12=9/36)
* The result is 8/36 + 9/36
* Add the numerators and put the sum over the LCD = 17/36
* Simplify the fraction if possible. In this case it is not possible
Multiplying Fractions
To Multiply Fractions:
* Multiply the numerators of the fractions
* Multiply the denominators of the fractions
* Place the product of the numerators over the product of the denominators
* Simplify the Fraction
Example: Multiply 2/9 and 3/12
* Multiply the numerators (2*3=6)
* Multiply the denominators (9*12=108)
* Place the product of the numerators over the product of the denominators (6/108)
* Simplify the Fraction (6/108 = 1/18)
*
* The Easy Way. It is often simplest to "cancel" before doing the multiplication. Canceling is dividing one factor of the numerator and one factor of the denominator by the same number.
* For example: 2/9 * 3/12 = (2*3)/(9*12) = (1*3)/(9*6) = (1*1)/(3*6) = 1/18
Multiplying Fractions by Whole Numbers
* Multiplying a fraction by an integer follows the same rules as multiplying two fractions.
* An integer can be considered to be a fraction with a denominator of 1.
* Therefore when a fraction is multiplied by an integer the numerator of the fraction is multiplied by the integer.
* The denominator is multiplied by 1 which does not change the denominator.
Dividing Fractions by Whole Numbers
To Divide Fractions by Whole Numbers:
* Treat the integer as a fraction (i.e. place it over the denominator 1)
* Invert (i.e. turn over) the denominator fraction and multiply the fractions
* Multiply the numerators of the fractions
* Multiply the denominators of the fractions
* Place the product of the numerators over the product of the denominators
* Simplify the Fraction
Example: Divide 2/9 by 2
* The integer divisor (2) can be considered to be a fraction (2/1)
* Invert the denominator fraction and multiply (2/9 ÷ 2/1 = 2/9 * 1/2)
* Multiply the numerators (2*1=2)
* Multiply the denominators (9*2=18)
* Place the product of the numerators over the product of the denominators (2/18)
* Simplify the Fraction if possible (2/18 = 1/9)
*
* The Easy Way. After inverting, it is often simplest to "cancel" before doing the multiplication. Canceling is dividing one factor of the numerator and one factor of the denominator by the same number.
* For example: 2/9 ÷ 2 = 2/9 ÷ 2/1 = 2/9*1/2 = (2*1)/(9*2) = (1*1)/(9*1) = 1/9
Dividing Fractions by Fractions
To Divide Fractions:
* Invert (i.e. turn over) the denominator fraction and multiply the fractions
* Multiply the numerators of the fractions
* Multiply the denominators of the fractions
* Place the product of the numerators over the product of the denominators
* Simplify the Fraction
Example: Divide 2/9 and 3/12
* Invert the denominator fraction and multiply (2/9 ÷ 3/12 = 2/9 * 12/3)
* Multiply the numerators (2*12=24)
* Multiply the denominators (9*3=27)
* Place the product of the numerators over the product of the denominators (24/27)
* Simplify the Fraction (24/27 = 8/9)
*
* The Easy Way. After inverting, it is often simplest to "cancel" before doing the multiplication. Canceling is dividing one factor of the numerator and one factor of the denominator by the same number.
* For example: 2/9 ÷ 3/12 = 2/9*12/3 = (2*12)/(9*3) = (2*4)/(3*3) = 8/9
Adding decimals
How to add Decimals that have different numbers of decimal places
* Write one number below the other so that the bottom decimal point is directly below and lined up with the top decimal point.
* Add each column starting at the right side.
Example: Add 3.2756 + 11.48
3.2756
11.48
14.7556
How to add three or more decimal numbers that have different numbers of decimal places.
* Write the numbers in a column so the decimal points are directly lined up.
* Add each column starting at the right side.
Example: Add 23.143 + 3.2756 + 11.48
23.143
3.2756
11.48
37.8986
Division of Decimals by Decimals
The procedure for the division of decimals is very similar to the division of whole numbers. Make the divisor into a whole number by multiplying both it and the dividend by the same number (such as 10, 100, 1000 etc.). An easy way to do this is to move the decimal point to the right end of the divisor and move the decimal point of the dividend the same number of places.
How to divide a four digit decimal number by a two digit decimal number (e.g 0.4131 ÷ 0.17).
* Place the divisor before the division bracket and place the dividend (0.4131) under it.
0.17)0.4131
* Multiply both the divisor and dividend by 100 so that the divisor is not a decimal but a whole number. In other words move the decimal point two places to the right in both the divisor and dividend
17)41.31
* Proceed with the division as you normally would except put the decimal point in the answer or quotient exactly above where it occurs in the dividend. For example:
2.43
17)41.31
Division of Decimals by Decimals
The procedure for the division of decimals is very similar to the division of whole numbers. Make the divisor into a whole number by multiplying both it and the dividend by the same number (such as 10, 100, 1000 etc.). An easy way to do this is to move the decimal point to the right end of the divisor and move the decimal point of the dividend the same number of places.
How to divide a four digit decimal number by a two digit decimal number (e.g. 0.424 ÷ 0.8).
* Place the divisor before the division bracket and place the dividend (0.424) under it.
0.8)0.424
* Multiply both the divisor and dividend by 10 so that the divisor is not a decimal but a whole number. In other words move the decimal point one place to the right in both the divisor and dividend
8)4.24
* Proceed with the division as you normally would except put the decimal point in the answer or quotient exactly above where it occurs in the dividend. For example:
0.53
8)4.24
4 0
24
0
Ordering Decimal Numbers
Numbers have an order or arrangement. The number two is between one and three. Three or more numbers can be placed in order. A number may come before the other numbers or it may come between them or after them.
Example: If we start with the numbers 4.3 and 8.78, the number 5.2764 would come between them, the number 9.1 would come after them and the number 2 would come before both of them.
Example: If we start with the numbers 4.3 and 4.78, the number 4.2764 would come before both of them, the number 4.9 would come after them and the number 4.5232 would come between them.
The order may be ascending (getting larger in value) or descending (becoming smaller in value).
Rounding Decimals
27.17469 rounded to the nearest whole number is 27
36.74691 rounded to the nearest whole number is 37
12.34690 rounded to the nearest tenth is 12.3
89.46917 rounded to the nearest tenth is 89.5
50.02139 rounded to the nearest hundredth is 50.02
72.63539 rounded to the nearest hundredth is 72.64
46.83531 rounded to the nearest thousandth is 46.835
9.63967 rounded to the nearest thousandth is 9.640
Rules for rounding decimals.
1. Retain the correct number of decimal places (e.g. 3 for thousandths, 0 for whole numbers)
2. If the next decimal place value is 5 or more, increase the value in the last retained decimal place by 1.
Estimate the difference between two decimals
How to Estimate a difference by rounding.
* Round each decimal term that will be subtracted.
* Subtract the rounded terms
Example: Estimate the difference of 0.988 - 0.53
* Round 0.988 - 0.53 to 1 - 0.5
* Subtract the rounded numbers to obtain the estimated difference of 0.5
* The actual difference of 0.988 - 0.53 is 0.458
Some uses of rounding are:
* Checking to see if you have enough money to buy what you want.
* Getting a rough idea of the correct answer to a problem
Estimate the sum of two decimals
How to Estimate a sum by rounding.
* Round each decimal term that will be added.
* Add the rounded terms
Example: Estimate the sum of 0.988 + 0.53
* Round 0.988 + 0.53 to 1 + 0.5
* Add the rounded numbers to obtain the estimated sum of 1.5
* The actual sum of 0.988 + 0.53 is 1.518
Some uses of rounding are:
* Checking to see if you have enough money to buy what you want.
* Getting a rough idea of the correct answer to a problem
Reciprocals
The product of a number and its reciprocal equals 1.
The reciprocal of 4 is 1/4.
The reciprocal of 2/3 is 3/2.
The reciprocal of 1 is 1.
The number 0 does not have a reciprocal because the product of any number and 0 equals 0.
Multiplying Mixed Numbers
Mixed numbers consist of an integer followed by a fraction.
* Multiplying two mixed numbers: Convert each mixed number to an improper fraction.
* Multiply the two numerators together.
* Multiply the two denominators together.
* Convert the result back to a mixed number if it is an improper fraction.
* Simplify the mixed number.
Example: 6 2/8 * 3 5/9 =

Fractions, Decimals and Percents
Finding the Percent of a Number
To determine the percent of a number do the following steps:
* Multiply the number by the percent (e.g. 87 * 68 = 5916)
* Divide the answer by 100 (Move decimal point two places to the left) (e.g. 5916/100 = 59.16)
* Round to the desired precision (e.g. 59.16 rounded to the nearest whole number = 59)
Converting a Percent to a Fraction
Do the following steps to convert a percent to a fraction:
For example: Convert 83% to a fraction.
* Remove the Percent sign
* Make a fraction with the percent as the numerator and 100 as the denominator (e.g. 83/100)
* Reduce the fraction if needed
Converting a Decimal to a Percent
Do the following steps to convert a decimal to a percent:
For example: Convert 0.83 to a percent.
* Multiply the decimal by 100 (e.g. 0.83 * 100 = 83)
* Add a percent sign after the answer (e.g. 83%)
Converting a Percent to a Decimal
How to convert a percent to a decimal:
For example: Convert 83% to a decimal.
* Divide the percent by 100 (e.g. 83 ÷ 100 = 0.83)
Comparing Decimals and Fractions
A decimal number and a fractional number can be compared. One number is either greater than, less than or equal to the other number.
When comparing fractional numbers to decimal numbers, convert the fraction to a decimal number by division and compare the decimal numbers.
To compare decimal numbers, start with tenths and then hundredths etc. If one decimal has a higher number in the tenths place then it is larger and the decimal with less tenths is smaller. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare.
It is often easy to estimate the decimal from a fraction. If this estimated decimal is obviously much larger or smaller than the compared decimal then it is not necessary to precisely convert the fraction to a decimal
Comparing Decimals and Fractions
A decimal number and a fractional number can be compared. One number is either greater than, less than or equal to the other number.
When comparing fractional numbers to decimal numbers, convert the fraction to a decimal number by division and compare the decimal numbers.
If one decimal has a higher number on the left side of the decimal point then it is larger. If the numbers to the left of the decimal point are equal but one decimal has a higher number in the tenths place then it is larger and the decimal with less tenths is smaller. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare.
It is often easy to estimate the decimal from a fraction. If this estimated decimal is obviously much larger or smaller than the compared decimal then it is not necessary to convert the fraction to a decimal
Comparing Whole Numbers and Fractions
An integer and a fractional number can be compared. One number is either greater than, less than or equal to the other number.
When comparing fractional numbers to whole number, convert the fraction to a decimal number by division and compare the numbers.
To compare decimal numbers to a whole number, start with the integer portion of the numbers. If one is larger then that one is the larger number. If they have the same value, compare tenths and then hundredths etc. If one decimal has a higher number in the tenths place then it is larger and the decimal with less tenths is smaller. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare.
To determine the percent of a number do the following steps:
* Multiply the number by the percent (e.g. 87 * 68 = 5916)
* Divide the answer by 100 (Move decimal point two places to the left) (e.g. 5916/100 = 59.16)
* Round to the desired precision (e.g. 59.16 rounded to the nearest whole number = 59)
Converting a Percent to a Fraction
Do the following steps to convert a percent to a fraction:
For example: Convert 83% to a fraction.
* Remove the Percent sign
* Make a fraction with the percent as the numerator and 100 as the denominator (e.g. 83/100)
* Reduce the fraction if needed
Converting a Decimal to a Percent
Do the following steps to convert a decimal to a percent:
For example: Convert 0.83 to a percent.
* Multiply the decimal by 100 (e.g. 0.83 * 100 = 83)
* Add a percent sign after the answer (e.g. 83%)
Converting a Percent to a Decimal
How to convert a percent to a decimal:
For example: Convert 83% to a decimal.
* Divide the percent by 100 (e.g. 83 ÷ 100 = 0.83)
Comparing Decimals and Fractions
A decimal number and a fractional number can be compared. One number is either greater than, less than or equal to the other number.
When comparing fractional numbers to decimal numbers, convert the fraction to a decimal number by division and compare the decimal numbers.
To compare decimal numbers, start with tenths and then hundredths etc. If one decimal has a higher number in the tenths place then it is larger and the decimal with less tenths is smaller. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare.
It is often easy to estimate the decimal from a fraction. If this estimated decimal is obviously much larger or smaller than the compared decimal then it is not necessary to precisely convert the fraction to a decimal
Comparing Decimals and Fractions
A decimal number and a fractional number can be compared. One number is either greater than, less than or equal to the other number.
When comparing fractional numbers to decimal numbers, convert the fraction to a decimal number by division and compare the decimal numbers.
If one decimal has a higher number on the left side of the decimal point then it is larger. If the numbers to the left of the decimal point are equal but one decimal has a higher number in the tenths place then it is larger and the decimal with less tenths is smaller. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare.
It is often easy to estimate the decimal from a fraction. If this estimated decimal is obviously much larger or smaller than the compared decimal then it is not necessary to convert the fraction to a decimal
Comparing Whole Numbers and Fractions
An integer and a fractional number can be compared. One number is either greater than, less than or equal to the other number.
When comparing fractional numbers to whole number, convert the fraction to a decimal number by division and compare the numbers.
To compare decimal numbers to a whole number, start with the integer portion of the numbers. If one is larger then that one is the larger number. If they have the same value, compare tenths and then hundredths etc. If one decimal has a higher number in the tenths place then it is larger and the decimal with less tenths is smaller. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare.
Division
Division
How to divide a three digit number by a one digit number (e.g 413 ÷ 7).
* Place the divisor before the division bracket and place the dividend (413) under it.
7)413
* Examine the first digit of the dividend(4). It is smaller than 7 so it can't be divided by 7 to produce a whole number. Next take the first two digits of the dividend (41) and determine how many 7's it contains. In this case 41 holds five sevens (5*7=35) but not six (6*7=42). Place the 5 above the division bracket.
5
7)413
* Multiply the 5 by 7 and place the result (35) below the 41 of the dividend.
5
7)413
35
* Draw a line under the 35 and subtract it from 41 (41-35=6). Bring down the 3 from the 413 and place it to the right of the 6.
5
7)413
35
63
* Divide 63 by 7 and place that answer above the division bracket to the right of the five.
59
7)413
35
63
* Multiply the 9 of the quotient by the divisor (7) to get 63 and place this below the 63 under the dividend. Subtract 63 from 63 to give an answer of 0. This indicates that there is nothing left over and 7 can be evenly divided into 413 to produce a quotient of 59.
59
7)413
35
63
63
0
How to divide a three digit number by a one digit number (e.g. 416 ÷ 7).
* Place the divisor before the division bracket and place the dividend (416) under it.
7)416
* Examine the first digit of the dividend(4). It is smaller than 7 so it can't be divided by 7 to produce a whole number. Next take the first two digits of the dividend (41) and determine how many 7's it contains. In this case 41 holds five sevens (5*7=35) but not six (6*7=42). Place the 5 above the division bracket.
5
7)416
* Multiply the 5 by 7 and place the result (35) below the 41 of the dividend.
5
7)416
35
* Draw a line under the 35 and subtract it from 41 (41-35=6). Bring down the 6 from the 416 and place it to the right of the other 6.
5
7)416
35
66
* Divide 66 by 7 and place that answer above the division bracket to the right of the five.
59
7)416
35
66
* Multiply the 9 of the quotient by the divisor (7) to get 63 and place this below the 66. Subtract 63 from 66 to give an answer of 3. The number 3 is called the remainder and indicates that there were three left over.
59 R 3
7)416
35
66
63
3
Division
Dividing a three digit number by a one digit number (for example 416 ÷ 7) involves several steps.
* Place the divisor before the division bracket and place the dividend (416) under it.
7)416
* Examine the first digit of the dividend(4). It is smaller than 7 so can't be divided by 7 to produce a whole number. Next take the first two digits of the dividend (41) and determine how many 7's it contains. In this case 41 holds five sevens (5*7=35) but not six (6*7=42). Place the 5 above the division bracket.
5
7)416
* Multiply the 5 by 7 and place the result (35) below the 41 of the dividend.
5
7)416
35
* Draw a line under the 35 and subtract it from 41 (41-35=6). Bring down the 6 from the 416 and place it to the right of the other 6.
5
7)416
35
66
* Divide 66 by 7 and place that answer above the division bracket to the right of the five.
59
7)416
35
66
* Multiply the 9 of the quotient by the divisor (7) to get 63 and place this below the 66. Subtract 63 from 66 to give an answer of 3. The number 3 is called the remainder and indicates that there were three left over.
59 R 3
7)416
35
66
63
3
Division
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 72 ÷ 8 = 9.
One of the terms in an equation may not be known and needs to be determined. The unknown term may be represented by a letter such as x. (e.g. x ÷ 8 = 9).
The solution of an equation is finding the value of the unknown x. Use the multiplication property of equations to find the value of x. The multiplication property property of equations states that the two sides of an equation remain equal if both sides are multiplied by the same number
Example:
x ÷ 5 = 2
x ÷ 5 * 5 = 2 * 5
x ÷ 1 = 10
x = 10
Check the answer by substituting the answer (10) back into the equation.
10 ÷ 5 = 2
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 132 ÷ 12 = 11.
One of the terms in an equation may not be known and needs to be determined. The unknown term may be represented by a letter such as x. (e.g. x ÷ 12 = 11).
The solution of an equation is finding the value of the unknown x. Use the multiplication property of equations to find the value of x. The multiplication property property of equations states that the two sides of an equation remain equal if both sides are multiplied by the same number
Example:
x ÷ 50 = 20
x ÷ 50 * 50 = 20 * 50
x ÷ 1 = 1000
x = 1000
Check the answer by substituting the answer (1000) back into the equation.
1000 ÷ 50 = 20
How to divide a three digit number by a one digit number (e.g 413 ÷ 7).
* Place the divisor before the division bracket and place the dividend (413) under it.
7)413
* Examine the first digit of the dividend(4). It is smaller than 7 so it can't be divided by 7 to produce a whole number. Next take the first two digits of the dividend (41) and determine how many 7's it contains. In this case 41 holds five sevens (5*7=35) but not six (6*7=42). Place the 5 above the division bracket.
5
7)413
* Multiply the 5 by 7 and place the result (35) below the 41 of the dividend.
5
7)413
35
* Draw a line under the 35 and subtract it from 41 (41-35=6). Bring down the 3 from the 413 and place it to the right of the 6.
5
7)413
35
63
* Divide 63 by 7 and place that answer above the division bracket to the right of the five.
59
7)413
35
63
* Multiply the 9 of the quotient by the divisor (7) to get 63 and place this below the 63 under the dividend. Subtract 63 from 63 to give an answer of 0. This indicates that there is nothing left over and 7 can be evenly divided into 413 to produce a quotient of 59.
59
7)413
35
63
63
0
How to divide a three digit number by a one digit number (e.g. 416 ÷ 7).
* Place the divisor before the division bracket and place the dividend (416) under it.
7)416
* Examine the first digit of the dividend(4). It is smaller than 7 so it can't be divided by 7 to produce a whole number. Next take the first two digits of the dividend (41) and determine how many 7's it contains. In this case 41 holds five sevens (5*7=35) but not six (6*7=42). Place the 5 above the division bracket.
5
7)416
* Multiply the 5 by 7 and place the result (35) below the 41 of the dividend.
5
7)416
35
* Draw a line under the 35 and subtract it from 41 (41-35=6). Bring down the 6 from the 416 and place it to the right of the other 6.
5
7)416
35
66
* Divide 66 by 7 and place that answer above the division bracket to the right of the five.
59
7)416
35
66
* Multiply the 9 of the quotient by the divisor (7) to get 63 and place this below the 66. Subtract 63 from 66 to give an answer of 3. The number 3 is called the remainder and indicates that there were three left over.
59 R 3
7)416
35
66
63
3
Division
Dividing a three digit number by a one digit number (for example 416 ÷ 7) involves several steps.
* Place the divisor before the division bracket and place the dividend (416) under it.
7)416
* Examine the first digit of the dividend(4). It is smaller than 7 so can't be divided by 7 to produce a whole number. Next take the first two digits of the dividend (41) and determine how many 7's it contains. In this case 41 holds five sevens (5*7=35) but not six (6*7=42). Place the 5 above the division bracket.
5
7)416
* Multiply the 5 by 7 and place the result (35) below the 41 of the dividend.
5
7)416
35
* Draw a line under the 35 and subtract it from 41 (41-35=6). Bring down the 6 from the 416 and place it to the right of the other 6.
5
7)416
35
66
* Divide 66 by 7 and place that answer above the division bracket to the right of the five.
59
7)416
35
66
* Multiply the 9 of the quotient by the divisor (7) to get 63 and place this below the 66. Subtract 63 from 66 to give an answer of 3. The number 3 is called the remainder and indicates that there were three left over.
59 R 3
7)416
35
66
63
3
Division
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 72 ÷ 8 = 9.
One of the terms in an equation may not be known and needs to be determined. The unknown term may be represented by a letter such as x. (e.g. x ÷ 8 = 9).
The solution of an equation is finding the value of the unknown x. Use the multiplication property of equations to find the value of x. The multiplication property property of equations states that the two sides of an equation remain equal if both sides are multiplied by the same number
Example:
x ÷ 5 = 2
x ÷ 5 * 5 = 2 * 5
x ÷ 1 = 10
x = 10
Check the answer by substituting the answer (10) back into the equation.
10 ÷ 5 = 2
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 132 ÷ 12 = 11.
One of the terms in an equation may not be known and needs to be determined. The unknown term may be represented by a letter such as x. (e.g. x ÷ 12 = 11).
The solution of an equation is finding the value of the unknown x. Use the multiplication property of equations to find the value of x. The multiplication property property of equations states that the two sides of an equation remain equal if both sides are multiplied by the same number
Example:
x ÷ 50 = 20
x ÷ 50 * 50 = 20 * 50
x ÷ 1 = 1000
x = 1000
Check the answer by substituting the answer (1000) back into the equation.
1000 ÷ 50 = 20
Multiplication
Multiplying two digit by one digit numbers
How to multiply a two digit number by a one digit number
(for example 59 + 7).
* Place one number above the other so that the ones' place digits are lined up. Draw a line under the bottom number.
59
7
* Multiply the two ones' place digits (9 * 7 = 63). This number is larger than 9, so place the six above the tens' place column and place the three below the line in the ones' place column.
6
59
7
3
* Multiply the digit in the tens' place column (5) by the second number (7). The result is 5 * 7 = 35. Add the 6 to the 35 (35 + 6 = 41) and place the answer below the line and to the left of the 3.
59
7
413
Multiplying three digit by one digit numbers
How to multiply a three digit number by a one digit number
(e.g. 159 * 7).
* Place one number above the other so that the ones' place digits are lined up. Draw a line under the bottom number.
159
7
* Multiply the two ones' place digits (9 * 7 = 63). This number is larger than 9, so place the six above the tens' place column and place the three below the line in the ones' place column.
6
159
7
3
* Multiply the digit in the tens' place column (5) by the other number (7). The result is 5 * 7 = 35. Add the 6 to the 35 which equals 41. Place the one from the number 41 below the line and to the left of the other number. Place the 4 above the hundreds' place column.
46
159
7
13
* Multiply the digit in the hundreds' place column (1) by the digit in the ones' place of the second number (7). The result is 1 * 7 = 7. Add the 4 to the 7 (4 + 7 = 11). Place this below the line and to the left of the other digits.
46
159
7
1113
Multiplying Three Numbers
How to multiply three numbers:
* Multiply the first number by the second number.
* Multiply the product of the first multiplication by the third number.
Multiplication of Two and Three Digit Numbers
How to multiply a three digit number by a two digit number (e.g. 529 * 67).
* Place one number above the other so that the hundreds', tens' and ones' places are lined up. Draw a line under the bottom number.
529
67
* Multiply the two numbers in the ones' places. (9 * 7 = 63). This number is larger than 9 so place a 6 above the tens' place column and place 3 below the line in the ones' place column.
6
529
67
3
* Muliply the digit in the top tens' place column (2) by the digit in the lower ones' place column (7). The answer (2*7=14) is added to the 6 above the top tens' place column to give an answer of 20. The 0 of 20 is placed below the line and the 2 of the 20 is placed above the hundreds' place column.
26
529
67
03
* The hundreds' place of the top number (5) is multiplied by the ones' place of the multiplier (5*7=35). The two that was previously carried to the hundreds' place is added and the 37 is placed below the line.
26
529
67
3703
* After 529 has been multiplied by 7 as shown above, 529 is multiplied by the tens' place of the multiplier which is 6. The number is moved one place to the left because we are multiplying by a tens' place number. The result would be 3174:
15
529
67
3703
3174
* A line is drawn under the lower product (3174) and the products are added together to get the final answer of 35443.
15
529
67
3703
3174
35443
Multiplication of Five Digit Numbers
Multiplying a five digit number by a one digit number (for example 52639 * 7) is illustrated below.
* Place one number above the other so that the one's places are lined up. Draw a line under the bottom number.
52639
7
368473
Multiplication of Five Digit Numbers.
Multiplying a five digit number by a two digit number (for example 52639 * 67) is illustrated below.
* Place one number above the other so that the hundred's, ten's and one's places are lined up. Draw a line under the bottom number.
52639
67
368473
315834
3526813
Multiplication of Five Digit Numbers
Multiplying a Five digit number by a three digit number (for example 24639 * 687) is illustrated below.
* Place one number above the other so that the hundred's, ten's and one's places are lined up. Draw a line under the bottom number.
24639
687
172473
197112
147834
16926993
Multiplying a Five digit number
Multiplying a Five digit number by a 4 digit number (for example 24639 * 3687) is illustrated below.
* Place one number above the other so that the thousand's, hundred's, ten's and one's places are lined up. Draw a line under the bottom number.
24639
3687
172473
197112
147834
73917
90843993
Multiplication of Six Digit Numbers.
Multiplying a six digit number by a two digit number (for example 524639 * 67) is illustrated below.
* Place one number above the other so that the hundred's, ten's and one's places are lined up. Draw a line under the bottom number.
524639
67
3672473
3147834
35150813
Multiplying a six digit number
Multiplying a six digit number by a three digit number (for example 524639 * 687) is illustrated below.
* Place one number above the other so that the hundred's, ten's and one's places are lined up. Draw a line under the bottom number.
524639
687
3672473
4197112
3147834
360426993
Multiplication Equations
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 9 * 8 = 72.
One of the terms in an equation may not be known and needs to be determined. The unknown term may be represented by a letter such as x. (e.g. x * 8 = 72).
The solution of an equation is finding the value of the unknown x. Use the division property of equations to find the value of x. The division property of equations states that the two sides of an equation remain equal if both sides are divided by the same number
Example:
x * 5 = 10
x * 5 ÷ 5 = 10 ÷ 5
x * 1 = 2
x = 2
Check the answer by substituting the answer (2) back into the equation.
2 * 5 = 10
Multiplication Equations
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 12 * 11 = 132.
One of the terms in an equation may not be known and needs to be determined. The unknown term may be represented by a letter such as x. (e.g. x * 11 = 132).
The solution of an equation is finding the value of the unknown x. Use the division property of equations to find the value of x. The division property of equations states that the two sides of an equation remain equal if both sides are divided by the same number
Example:
x * 50 = 1000
x * 50 ÷ 50 = 1000 ÷ 50
x * 1 = 20
x = 20
Check the answer by substituting the answer (20) back into the equation.
20 * 50 = 1000
How to multiply a two digit number by a one digit number
(for example 59 + 7).
* Place one number above the other so that the ones' place digits are lined up. Draw a line under the bottom number.
59
7
* Multiply the two ones' place digits (9 * 7 = 63). This number is larger than 9, so place the six above the tens' place column and place the three below the line in the ones' place column.
6
59
7
3
* Multiply the digit in the tens' place column (5) by the second number (7). The result is 5 * 7 = 35. Add the 6 to the 35 (35 + 6 = 41) and place the answer below the line and to the left of the 3.
59
7
413
Multiplying three digit by one digit numbers
How to multiply a three digit number by a one digit number
(e.g. 159 * 7).
* Place one number above the other so that the ones' place digits are lined up. Draw a line under the bottom number.
159
7
* Multiply the two ones' place digits (9 * 7 = 63). This number is larger than 9, so place the six above the tens' place column and place the three below the line in the ones' place column.
6
159
7
3
* Multiply the digit in the tens' place column (5) by the other number (7). The result is 5 * 7 = 35. Add the 6 to the 35 which equals 41. Place the one from the number 41 below the line and to the left of the other number. Place the 4 above the hundreds' place column.
46
159
7
13
* Multiply the digit in the hundreds' place column (1) by the digit in the ones' place of the second number (7). The result is 1 * 7 = 7. Add the 4 to the 7 (4 + 7 = 11). Place this below the line and to the left of the other digits.
46
159
7
1113
Multiplying Three Numbers
How to multiply three numbers:
* Multiply the first number by the second number.
* Multiply the product of the first multiplication by the third number.
Multiplication of Two and Three Digit Numbers
How to multiply a three digit number by a two digit number (e.g. 529 * 67).
* Place one number above the other so that the hundreds', tens' and ones' places are lined up. Draw a line under the bottom number.
529
67
* Multiply the two numbers in the ones' places. (9 * 7 = 63). This number is larger than 9 so place a 6 above the tens' place column and place 3 below the line in the ones' place column.
6
529
67
3
* Muliply the digit in the top tens' place column (2) by the digit in the lower ones' place column (7). The answer (2*7=14) is added to the 6 above the top tens' place column to give an answer of 20. The 0 of 20 is placed below the line and the 2 of the 20 is placed above the hundreds' place column.
26
529
67
03
* The hundreds' place of the top number (5) is multiplied by the ones' place of the multiplier (5*7=35). The two that was previously carried to the hundreds' place is added and the 37 is placed below the line.
26
529
67
3703
* After 529 has been multiplied by 7 as shown above, 529 is multiplied by the tens' place of the multiplier which is 6. The number is moved one place to the left because we are multiplying by a tens' place number. The result would be 3174:
15
529
67
3703
3174
* A line is drawn under the lower product (3174) and the products are added together to get the final answer of 35443.
15
529
67
3703
3174
35443
Multiplication of Five Digit Numbers
Multiplying a five digit number by a one digit number (for example 52639 * 7) is illustrated below.
* Place one number above the other so that the one's places are lined up. Draw a line under the bottom number.
52639
7
368473
Multiplication of Five Digit Numbers.
Multiplying a five digit number by a two digit number (for example 52639 * 67) is illustrated below.
* Place one number above the other so that the hundred's, ten's and one's places are lined up. Draw a line under the bottom number.
52639
67
368473
315834
3526813
Multiplication of Five Digit Numbers
Multiplying a Five digit number by a three digit number (for example 24639 * 687) is illustrated below.
* Place one number above the other so that the hundred's, ten's and one's places are lined up. Draw a line under the bottom number.
24639
687
172473
197112
147834
16926993
Multiplying a Five digit number
Multiplying a Five digit number by a 4 digit number (for example 24639 * 3687) is illustrated below.
* Place one number above the other so that the thousand's, hundred's, ten's and one's places are lined up. Draw a line under the bottom number.
24639
3687
172473
197112
147834
73917
90843993
Multiplication of Six Digit Numbers.
Multiplying a six digit number by a two digit number (for example 524639 * 67) is illustrated below.
* Place one number above the other so that the hundred's, ten's and one's places are lined up. Draw a line under the bottom number.
524639
67
3672473
3147834
35150813
Multiplying a six digit number
Multiplying a six digit number by a three digit number (for example 524639 * 687) is illustrated below.
* Place one number above the other so that the hundred's, ten's and one's places are lined up. Draw a line under the bottom number.
524639
687
3672473
4197112
3147834
360426993
Multiplication Equations
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 9 * 8 = 72.
One of the terms in an equation may not be known and needs to be determined. The unknown term may be represented by a letter such as x. (e.g. x * 8 = 72).
The solution of an equation is finding the value of the unknown x. Use the division property of equations to find the value of x. The division property of equations states that the two sides of an equation remain equal if both sides are divided by the same number
Example:
x * 5 = 10
x * 5 ÷ 5 = 10 ÷ 5
x * 1 = 2
x = 2
Check the answer by substituting the answer (2) back into the equation.
2 * 5 = 10
Multiplication Equations
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 12 * 11 = 132.
One of the terms in an equation may not be known and needs to be determined. The unknown term may be represented by a letter such as x. (e.g. x * 11 = 132).
The solution of an equation is finding the value of the unknown x. Use the division property of equations to find the value of x. The division property of equations states that the two sides of an equation remain equal if both sides are divided by the same number
Example:
x * 50 = 1000
x * 50 ÷ 50 = 1000 ÷ 50
x * 1 = 20
x = 20
Check the answer by substituting the answer (20) back into the equation.
20 * 50 = 1000
Subtraction
Subtracting five Digit Numbers
Subtracting two five digit numbers (for example 94,529 - 76,733) is illustrated
834
94529
76733
17796
Subtraction equations - 5 digit
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 60000 - 40000 = 20000.
One of the terms in an equation may not be know and needs to be determined. Often this unknown term is represented by a letter such as x. (e.g. x - 40000 = 20000).
The solution of an equation is finding the value of the unknown x. To find the value of x we can use the additive equation property which says: The two sides of an equation remain equal if the same number is added to each side.
Example:
x - 50000 = 70000
x - 50000 + 50000 = 70000 + 50000
x - 0 = 120000
x = 120000
Check the answer by substituting the value of x (120000) back into the equation.
120000 - 50000 = 70000
Adding Four Digit Numbers
How to add four digit numbers (for example 4529 + 6733):
* Place one number above the other so that the thousands', hundreds', tens' and ones' places are lined up. Draw a line under the bottom number.
4529
6733
* Add the ones' place digits (9 + 3 = 12). This number is larger than 10 so place a one above the tens' place column and place the two below the line in the ones' place column.
1
4529
6733
2
* Add the tens' place digits (1 + 2 + 3 = 6) and place the answer below the line and in the tens' place column.
4529
6733
62
* Add the numbers in the hundreds' place column (5 + 7 = 12) and place the 2 below the line and before the other number below the line. Place the 1 from the twelve above the thousands' place column.
1
4529
6733
262
* Add the digits in the thousands' place column (1 + 4 + 6 = 11) and place the answer below the line in the thousands' place column.
4529
6733
11262
Subtraction equations - 6 digit
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 600000 - 400000 = 200000.
One of the terms in an equation may not be know and needs to be determined. Often this unknown term is represented by a letter such as x. (e.g. x - 400000 = 200000).
The solution of an equation is finding the value of the unknown x. To find the value of x we can use the additive equation property which says: The two sides of an equation remain equal if the same number is added to each side.
Example:
x - 500000 = 700000
x - 500000 + 500000 = 700000 + 500000
x - 0 = 1200000
x = 1200000
Check the answer by substituting the value of x (1200000) back into the equation.
1200000 - 500000 = 700000
Subtracting seven Digit Numbers
Subtracting two seven digit numbers (for example 8,694,529 - 3,476,733) is illustrated
834
8694529
3476733
5217796
Subtracting two five digit numbers (for example 94,529 - 76,733) is illustrated
834
94529
76733
17796
Subtraction equations - 5 digit
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 60000 - 40000 = 20000.
One of the terms in an equation may not be know and needs to be determined. Often this unknown term is represented by a letter such as x. (e.g. x - 40000 = 20000).
The solution of an equation is finding the value of the unknown x. To find the value of x we can use the additive equation property which says: The two sides of an equation remain equal if the same number is added to each side.
Example:
x - 50000 = 70000
x - 50000 + 50000 = 70000 + 50000
x - 0 = 120000
x = 120000
Check the answer by substituting the value of x (120000) back into the equation.
120000 - 50000 = 70000
Adding Four Digit Numbers
How to add four digit numbers (for example 4529 + 6733):
* Place one number above the other so that the thousands', hundreds', tens' and ones' places are lined up. Draw a line under the bottom number.
4529
6733
* Add the ones' place digits (9 + 3 = 12). This number is larger than 10 so place a one above the tens' place column and place the two below the line in the ones' place column.
1
4529
6733
2
* Add the tens' place digits (1 + 2 + 3 = 6) and place the answer below the line and in the tens' place column.
4529
6733
62
* Add the numbers in the hundreds' place column (5 + 7 = 12) and place the 2 below the line and before the other number below the line. Place the 1 from the twelve above the thousands' place column.
1
4529
6733
262
* Add the digits in the thousands' place column (1 + 4 + 6 = 11) and place the answer below the line in the thousands' place column.
4529
6733
11262
Subtraction equations - 6 digit
An equation is a mathematical statement such that the expression on the left side of the equals sign (=) has the same value as the expression on the right side. An example of an equation is 600000 - 400000 = 200000.
One of the terms in an equation may not be know and needs to be determined. Often this unknown term is represented by a letter such as x. (e.g. x - 400000 = 200000).
The solution of an equation is finding the value of the unknown x. To find the value of x we can use the additive equation property which says: The two sides of an equation remain equal if the same number is added to each side.
Example:
x - 500000 = 700000
x - 500000 + 500000 = 700000 + 500000
x - 0 = 1200000
x = 1200000
Check the answer by substituting the value of x (1200000) back into the equation.
1200000 - 500000 = 700000
Subtracting seven Digit Numbers
Subtracting two seven digit numbers (for example 8,694,529 - 3,476,733) is illustrated
834
8694529
3476733
5217796
Subscribe to:
Comments (Atom)